给一个长度为 的序列 ,和 组询问 ,表示求 的值。实数输出,精度要求 。
。
2020-12-16
一个长度为 的排列是正确的,当且仅当他不存在非平凡的连续子序列,使得他的值也是连续的。 对于 求出,有多少长度为 的正确的排列。 。
2020-10-18
给定一个 个点的简单多边形(不保证是凸的),你需要确定一个半径 ,然后在每个端点画一个半径为 的圆,要求能覆盖简单多边形的全部面积。 你需要确定这个 最小是多少,精度要求 。 。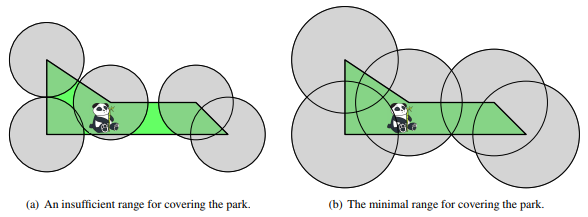
2020-10-04
给定 和 ,表示 条限制形如对于 满足 对于所有 。 其中 ,这里 都是整数,即 是一个不超过 次的整系数多项式。 问满足限制的 有多少个,答案对 取模。 ,。
2020-09-17
用三元组 表示长度为 的递增等差正整数序列 。给定 ,要求构造 满足: 。
2020-09-15
一个大小为 的集合 ,每次可以选择 ,若 且 ,可以将 删去。 求能删除最多数的删除序列数,删除序列定义为对于一个三元组 ,每次删数把 加入到删除序列中。 ,保证 两两不同。
2020-08-31
给定一张 个点的树或基环树,树上的每条边 代表 间有 道路相连。 你需要统计有多少种从任意点出发的本质不同路径,使得经过所有道路恰好一次。 路径可以认为是一个从某个点出发,由经过道路编号和方向组成的序列。两条路线被认为是相同的当且仅当两序列相同,或更换起始边后两序列相同。 。
2020-08-08
你有 个队列,每个队列有 的容量。 次操作,每次给定队列的区间 ,push 一个 。如果第 个队列的元素个数 ,会自动 pop。 要求每次操作后求出所有序列中本质不同的元素个数。 。
2020-08-02
给定两个长度 的序列 ,序列每一位是 或 。每次你可以选择一个长度 的区间进行左右翻转,代价为区间数值和加上给定常数 。问将 变换成 的最小代价。 。