从 到 的正整数各出现两次,共 个数,分布在 个大小至多为 的栈中。你可以进行至多 次如下操作:弹出一个栈的栈顶元素并压入另一个栈中,要求另一个栈是空的或该栈只有一个元素且该元素数值上等于要压入的元素。构造一个操作序列或报告无解,要求操作结束后的 个栈满足栈要么为空要么恰包含两个相同的数。
。
2025-05-07
从 到 的正整数各出现两次,共 个数,分布在 个大小至多为 的栈中。你可以进行至多 次如下操作:弹出一个栈的栈顶元素并压入另一个栈中,要求另一个栈是空的或该栈只有一个元素且该元素数值上等于要压入的元素。构造一个操作序列或报告无解,要求操作结束后的 个栈满足栈要么为空要么恰包含两个相同的数。 。
2024-03-26
主办方将在一个二维平面中投放广告。共有 个广告可被投放,其中每个广告的都是左上角为 的 矩形且出现时间为 。同一时间内,任意两个被投放的广告不能有重叠面积。此外还有 条限制 表示在广告 和广告 中至少选择投放一条。判断是否存在一组合法的投放方案,如果存在的话给出方案。 ,,。
2023-11-08
维护一棵点有颜色的树,一开始只有编号为 的节点,其颜色为 ,要求支持以下操作 次: 每次操作后,你都需要在树上选两个颜色不同的点并最大化它们之间最短简单路径的长度,并输出。 。
2021-01-21
定义一个排列 上的操作 为: 现给定排列 ,要求使用至多 次如上操作,使 从小到大排序,注意你不需要最小化操作次数。 。
2020-12-16
一个长度为 的排列是正确的,当且仅当他不存在非平凡的连续子序列,使得他的值也是连续的。 对于 求出,有多少长度为 的正确的排列。 。
2020-10-18
给定一个 个点的简单多边形(不保证是凸的),你需要确定一个半径 ,然后在每个端点画一个半径为 的圆,要求能覆盖简单多边形的全部面积。 你需要确定这个 最小是多少,精度要求 。 。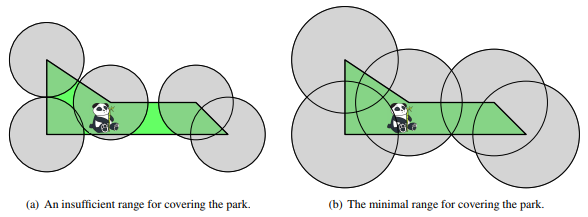
2020-10-04
给定 和 ,表示 条限制形如对于 满足 对于所有 。 其中 ,这里 都是整数,即 是一个不超过 次的整系数多项式。 问满足限制的 有多少个,答案对 取模。 ,。
2020-09-17
用三元组 表示长度为 的递增等差正整数序列 。给定 ,要求构造 满足: 。