「XX Open Cup. GP of Gomel」Hit

2020 年 07 月 31 日

给出 $n$ 个区间 $[l_i, r_i]$ ，你需要放下至多 $n$ 个点，使得每个区间里至少包含一个点。并且区间里点个数的最大值要尽可能小。

$1 \le n \le 10^5, 10^9 \le l_i < r_i \le 10^9$ 。

题解

先按照如下方法贪心：维护一个集合表示当前没有放点的区间，每次选出一个右端点最小的区间，在这个右端点放下一个区间。

若此时的最大值为 $t$ ，则答案要么为 $t$ 要么为 $t-1$ 。

证明：考虑一个被放了 $t$ 个点的区间，只有可能把第一个点的移到区间外，其余的点必定在区间内移动。

怎么判断答案是否为 $t-1$ 呢，定义一个点 $x$ 是合法的当且仅当只考虑 $x$ 和所有被放在 $x$ 右侧的点所有右端点 $r_i\geq x$ 的区间都能至多放 $t-1$ 个。

从右往左扫描线，定义 $next_x$ 为在 $x$ 右侧，能找到的最远合法点，且区间 $(x, next_x)$ 内不严格包含任意一个区间。令 $y=next^{t-1}_x$ ，如果不存在一个区间同时包含 $x, y$ ，那么 $x$ 就是合法的。

求出所有合法点后，若 $min_{i=1}^n (l_i)$ 是合法的，答案为 $t-1$ ，否则答案为 $t$ 。

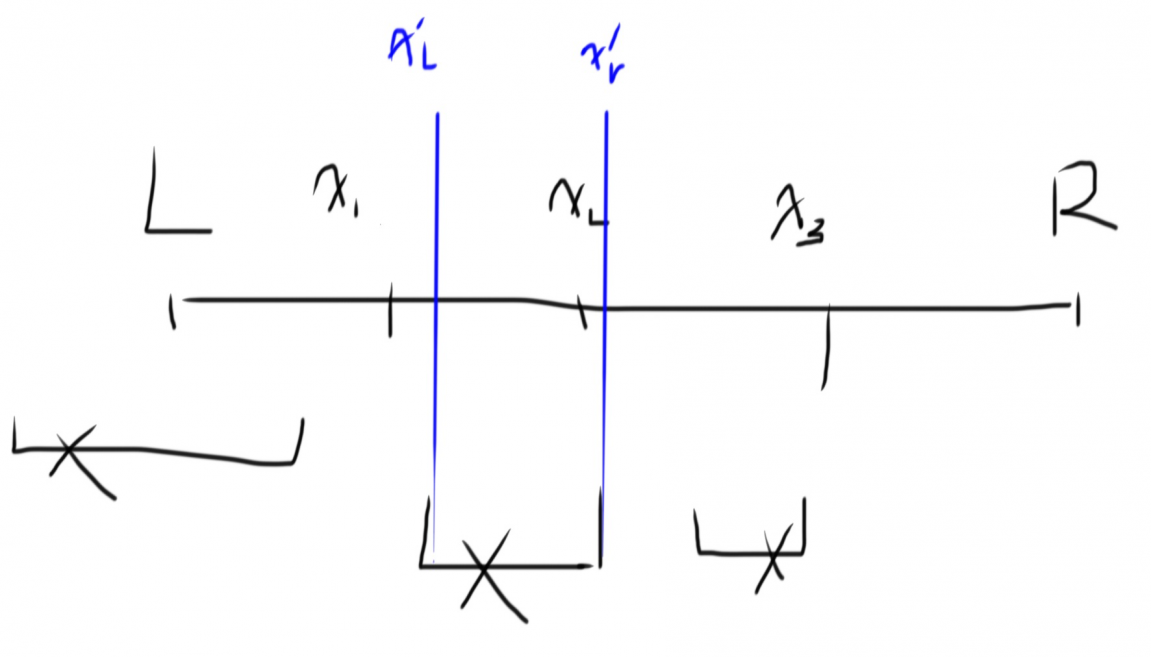
（附图：考虑我们是要让每个形如 $x_1$ 的贡献都丢到外面去，但是 $x'_1$ 能取的范围只能在 $[x'_l; x'_r]$ ，否则就不能完整覆盖内部线段）

坑

一开始调了半天就是离散化的问题。

实际上区间间留白的部分是有影响的（考虑是否完全包含的时候），把这部分也丢进去离散化就过了，哭哭。

不过别的部分能一遍写对还是挺开心的。

zimpha 的题解

考虑每个区间至少放一个点的贪心做法。维护一个集合表示当前没有放点的区间，每次选出一个右端点最小的区间，在这个右端点放下一个区间。

如果在上述方案下，最大值为 $t$ ，那么可以证明最优值要么是 $t$ ，要么是 $t-1$ 。

考虑上述方案下，包含点数最多的那个区间 $[l, r]$ 。假设这 $t$ 个点从左往右依次为 $x_1, x_2, \dots, x_t$ 。那么在最优方案下，这个区间里的点个数肯定要 $\le t$ 。考虑 $l$ 左边的第一个点为 $x^\prime_1$ ，那么接下来那个点 $x^\prime_2$ 一定要不超过 $x_2$ 。因为我们需要用 $x^\prime_2$ 来覆盖被 $x_1$ 覆盖的区间，如果超过 $x_2$ ，肯定会有区间没有被覆盖。类似的， $x^\prime_3$ 一定不能超过 $x_3$ 。依次类推， $x^\prime_t$ 一定不能超过 $x_t$ 。也就是少区间 $[l, r]$ 里至少要有 $t-1$ 个点。

那么接下来只需要判定 $t-1$ 是否可行即可。我们从左往右考虑数轴上每个点 $x$ ，定义 $x$ 是合法的当且仅当如果我们的方案包含了点 $x$ 后，仅考虑加入其它 $\ge x$ 的点，所有右端点 $r_i \ge x$ 的区间里面最多只有 $t-1$ 个点。令 $next(x)$ 是 $x$ 右边最远的合法的点，使得没有区间 $[l_i, r_i]$ 严格在区间 $[x, next_x]$ 里。考虑 $y=next^{t-1}(x)$ ，如果存在一个 $[l_i, r_i]$ 同时包含了端点 $x$ 和 $y$ ，那么 $x$ 显然是不合法的，否则 $x$ 是合法的。

最后如果所有点 $\min(l_i)-1$ 是合法的，那么就存在一个 $t-1$ 的解。

复杂度 $O(n \log n)$ 。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 9, M = 21;
int T, n, t, tn, ta[N], maxl[N], maxr[N], mrk[N], nxt[N][M];
vector<int> pos, ans;
struct node {
  int l, r;
} a[N];
struct segment {
  int l, r, mid, s;
} p[N << 2];
inline bool inside(int l, int r) { return l <= r && maxl[r] >= l; }
inline bool outside(int l, int r) { return l > r || maxr[l] >= r; }
void build(int u, int l, int r) {
  p[u].l = l, p[u].r = r, p[u].mid = (l + r) >> 1, p[u].s = 0;
  if (l == r) return;
  build(u << 1, l, p[u].mid);
  build(u << 1 | 1, p[u].mid + 1, r);
}
void modify(int u, int k, int x) {
  if (p[u].l == p[u].r) {
    p[u].s += x;
    return;
  }
  modify(k <= p[u].mid ? u << 1 : u << 1 | 1, k, x);
  p[u].s = p[u << 1].s + p[u << 1 | 1].s;
}
int query(int u, int l, int r) {
  if (p[u].l == l && p[u].r == r) return p[u].s;
  if (r <= p[u].mid) return query(u << 1, l, r);
  if (l > p[u].mid) return query(u << 1 | 1, l, r);
  return query(u << 1, l, p[u].mid) + query(u << 1 | 1, p[u].mid + 1, r);
}
int main() {
#ifdef memset0
  freopen("1.in", "r", stdin);
#endif
  cin.tie(0)->sync_with_stdio(0);
  for (cin >> T; T--;) {
    t = tn = 0, ans.clear(), pos.clear();
    cin >> n;
    ta[++tn] = 1e9 + 10, ta[++tn] = -1e9 - 10;
    for (int i = 1; i <= n; i++) {
      cin >> a[i].l, ta[++tn] = a[i].l;
      cin >> a[i].r, ta[++tn] = a[i].r;
      ta[++tn] = a[i].l - 1, ta[++tn] = a[i].l + 1;
      ta[++tn] = a[i].r - 1, ta[++tn] = a[i].r + 1;
    }
    sort(ta + 1, ta + tn + 1);
    tn = unique(ta + 1, ta + tn + 1) - ta - 1;
    for (int i = 1; i <= n; i++) {
      a[i].l = lower_bound(ta + 1, ta + tn + 1, a[i].l) - ta;
      a[i].r = lower_bound(ta + 1, ta + tn + 1, a[i].r) - ta;
    }
    memset(maxl + 1, 0, tn << 2);
    memset(maxr + 1, 0, tn << 2);
    for (int i = 1; i <= n; i++) {
      maxl[a[i].r] = max(maxl[a[i].r], a[i].l);
      maxr[a[i].l] = max(maxr[a[i].l], a[i].r);
    }
    for (int i = 1; i <= tn; i++) {
      maxl[i] = max(maxl[i - 1], maxl[i]);
      maxr[i] = max(maxr[i - 1], maxr[i]);
    }
    sort(a + 1, a + n + 1, [](const node &a, const node &b) { return a.r == b.r ? a.l < b.l : a.r < b.r; });
    build(1, 1, tn);
    for (int i = 1; i <= n; i++)
      if (!query(1, a[i].l, a[i].r)) {
        modify(1, a[i].r, 1);
        ans.push_back(a[i].r);
      }
    for (int i = 1; i <= n; i++) {
      t = max(t, query(1, a[i].l, a[i].r));
    }
    if (t > 1) {
      memset(mrk + 1, 0, tn);
      pos.push_back(tn), mrk[tn] = 1;
      for (int i = 0; i < M; i++) nxt[tn][i] = tn;
      for (int i = tn - 1, j, l, r, mid, s, k; i >= 1; i--) {
        l = 0, r = pos.size() - 1, nxt[i][0] = -1;
        while (l <= r) {
          mid = (l + r) >> 1;
          if (!inside(i + 1, pos[mid] - 1)) {
            nxt[i][0] = pos[mid];
            r = mid - 1;
          } else {
            l = mid + 1;
          }
        }
        if (!~nxt[i][0]) continue;
        for (j = nxt[i][0], k = M - 1, s = t - 2; k >= 0; k--) {
          if ((s >> k) & 1) j = nxt[j][k];
        }
        if (outside(i, j)) continue;
        pos.push_back(i), mrk[i] = 1;
        for (int j = 1; j < M; j++) {
          nxt[i][j] = nxt[nxt[i][j - 1]][j - 1];
        }
      }
      int minl = tn;
      for (int i = 1; i <= n; i++) minl = min(minl, a[i].l);
      if (mrk[minl - 1]) {
        --t, ans.clear();
        int u = minl - 1;
        while (u != tn) ans.push_back(u), u = nxt[u][0];
        if (ans.front() == 1) ans.erase(ans.begin());
      }
    }
    cout << t << ' ' << ans.size() << ' ';
    for (int i = 0; i < ans.size(); i++) {
      cout << ta[ans[i]] << " \n"[i + 1 == ans.size()];
    }
  }
}

TABLE OF CONTENTS

题解

坑

zimpha 的题解

代码

题解

坑

zimpha 的题解

代码

评论