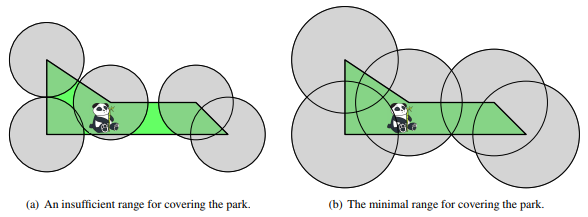
给定一个 个点的简单多边形(不保证是凸的),你需要确定一个半径 ,然后在每个端点画一个半径为 的圆,要求能覆盖简单多边形的全部面积。
你需要确定这个 最小是多少,精度要求 。
。
题解
考虑求出端点的 Voronoi 图,答案一定是由 Voronoi 图的端点,或者是 Voronoi 图和多边形的交点贡献的。由于这题数据范围较小,我们可以跑暴力半平面交。
Hack
正常做法中,我们知道 Voronoi 图实际上是把二维平面按照距离最近的关键点划分为若干部分,所以贡献答案的计算是容易的。
然而我们点开一看博主的代码:LibreOJ Submission #959701,发现他好像并不清楚 Voronoi 图的性质,而是大力猜想 Voronoi 图和原多边形的交点个数是 级别的,然后暴力跑贡献答案。看起来好像非常对,而且实际上跑的还很快。
但这个猜想嘛并不正确,怎么卡呢?我们考虑对交点个数计数:将我们把简单多边形的边提出来染色,若边上的一个区间和端点 距离最近,就染成染色 。那么总交点个数即等于每条边的颜色段数和。Hack 程序见后。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 9;
const double inf = 2e4, eps = 0;
namespace geometry {
const double mathPI = acos(-1);
template <class T> inline T abs(const T &x) { return x < 0 ? -x : x; }
struct point {
double x, y;
inline bool operator<(const point &rhs) const { return (abs(x - rhs.x) <= eps) ? (y - rhs.y < -eps) : (x - rhs.x < -eps); }
inline bool operator==(const point &rhs) const { return abs(x - rhs.x) <= eps && abs(y - rhs.y) <= eps; }
};
struct line {
point a, b;
inline bool operator<(const line &rhs) const { return a == rhs.a ? b < rhs.b : a < rhs.a; }
};
inline double squaredDistance(const point &a, const point &b) { return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y); }
inline double distance(const point &a, const point &b) { return sqrt(squaredDistance(a, b)); }
inline double cross(const point &u, const point &a, const point &b) { return (a.x - u.x) * (b.y - u.y) - (b.x - u.x) * (a.y - u.y); }
inline point intersect(const line &a, const line &b) {
double u = ((a.a.y - b.a.y) * (b.a.x - b.b.x) - (a.a.x - b.a.x) * (b.a.y - b.b.y)) / ((a.a.x - a.b.x) * (b.a.y - b.b.y) - (a.a.y - a.b.y) * (b.a.x - b.b.x));
return {u * (a.a.x - a.b.x) + a.a.x, u * (a.a.y - a.b.y) + a.a.y};
}
inline bool checkSegmentCrossed(const line &a, const line &b) { return ((cross(a.a, a.b, b.a) < eps) ^ (cross(a.a, a.b, b.b) < eps)) && ((cross(b.a, b.b, a.a) < eps) ^ (cross(b.a, b.b, a.b) < eps)); }
inline bool insideConvex(const point &x, const vector<point> &a) {
bool target = cross(a[0], a[1], x) < eps;
for (int i = 1; i < a.size(); i++)
if (target != (cross(a[i], a[(i + 1) % a.size()], x) < eps)) return false;
return true;
}
inline bool insidePolygon(const point &x, const vector<point> &a) {
vector<double> deg(a.size());
for (int i = 0; i < a.size(); i++) {
deg[i] = atan2(a[i].y - x.y, a[i].x - x.x);
}
double sum = 0;
for (int i = 0; i < a.size(); i++) {
double cur = deg[i] - deg[(i + 1) % a.size()];
if (cur >= mathPI) cur -= mathPI;
if (cur <= -mathPI) cur += mathPI;
sum += cur;
}
return abs(sum) > .5 * mathPI;
}
deque<point> halfPlane(const vector<line> &source) {
vector<pair<line, double>> plane(source.size());
for (int i = 0; i < plane.size(); i++) {
plane[i] = {source[i], atan2(source[i].b.y - source[i].a.y, source[i].b.x - source[i].a.x)};
}
sort(plane.begin(), plane.end(), [&](const pair<line, double> &a, const pair<line, double> &b) { return abs(a.second - b.second) > eps ? a.second < b.second : cross(a.first.a, b.first.a, b.first.b) > eps; });
deque<point> q;
deque<line> ql;
for (int i = 0; i < plane.size(); i++) {
if (i && abs(plane[i].second - plane[i - 1].second) <= eps) continue;
line cur = plane[i].first;
while (q.size() && cross(cur.a, cur.b, q.back()) < -eps) q.pop_back(), ql.pop_back();
while (q.size() && cross(cur.a, cur.b, q.front()) < -eps) q.pop_front(), ql.pop_front();
if (ql.size()) q.push_back(intersect(ql.back(), cur));
ql.push_back(cur);
}
while (q.size() > 1 && cross(ql.front().a, ql.front().b, q.back()) < -eps) q.pop_back(), ql.pop_back();
return q;
}
} // namespace geometry
using namespace geometry;
int n, satisifyCounter;
vector<point> a;
double ans;
set<point> voronoiNode;
set<line> voronoiEdge;
void satisifyNode(const point &x) {
if (isnan(x.x) || isnan(x.y)) return;
double cur = numeric_limits<double>::infinity();
for (int i = 0; i < n; i++) {
cur = min(cur, squaredDistance(x, a[i]));
}
++satisifyCounter;
ans = max(ans, cur);
}
int main() {
#ifdef memset0
freopen("1.in", "r", stdin);
#endif
cin.tie(0)->sync_with_stdio(0);
cin >> n;
a.resize(n);
for (int i = 0; i < n; i++) cin >> a[i].x >> a[i].y;
for (int i = 0; i < n; i++) satisifyNode({(a[i].x + a[(i + 1) % n].x) / 2, (a[i].y + a[(i + 1) % n].y) / 2});
for (int i = 0; i < n; i++) {
vector<line> plane = {
{{inf, inf}, {-inf, inf}},
{{inf, -inf}, {inf, inf}},
{{-inf, inf}, {-inf, -inf}},
{{-inf, -inf}, {inf, -inf}},
};
for (int j = 0; j < n; j++)
if (i != j) {
point mid{(a[i].x + a[j].x) / 2, (a[i].y + a[j].y) / 2};
point delta{a[i].x - mid.x, a[i].y - mid.y};
plane.push_back({{mid.x - delta.y, mid.y + delta.x}, {mid.x + delta.y, mid.y - delta.x}});
}
auto convex = halfPlane(plane);
for (int i = 0; i < convex.size(); i++) {
voronoiNode.insert(convex[i]);
line e = {convex[i], convex[(i + 1) % convex.size()]};
if (e.a.x < e.b.x) swap(e.a, e.b);
voronoiEdge.insert(e);
}
}
for (const point &x : voronoiNode) {
if (insidePolygon(x, a)) {
satisifyNode(x);
}
}
for (const line &e : voronoiEdge) {
for (int i = 0; i < a.size(); i++) {
line target{a[i], a[(i + 1) % a.size()]};
if (checkSegmentCrossed(e, target)) {
satisifyNode(intersect(e, target));
}
}
}
cout << fixed << setprecision(12) << sqrt(ans) << endl;
}Hack 程序
#include <bits/stdc++.h>
using namespace std;
int main() {
cin.tie(0)->sync_with_stdio(0);
const int lx = -10000, rx = -9000, ly = -10000, ry = 10000, m = 250;
vector<pair<int, int>> node;
for (int i = 1; i <= m; i++) {
node.push_back({rx, i * 2 - 1});
node.push_back({lx, i * 2 - 1});
node.push_back({lx, i * 2});
node.push_back({rx, i * 2});
}
for (int i = 1; i <= m; i++) {
node.push_back({rx + i * 2 - 1, ry});
node.push_back({rx + i * 2 - 1, ly});
if (i != m) {
node.push_back({rx + i * 2, ly});
node.push_back({rx + i * 2, ry});
} else {
node.push_back({rx + m * 2, ly - 1});
node.push_back({rx, ly - 1});
}
}
cout << node.size() << endl;
for (auto x : node) cout << x.first << " " << x.second << endl;
cout << endl;
}