VIII. 假设检验

本篇笔记介绍了数理统计中假设检验的基本概念和方法。首先讨论了两类错误（第 I 类错误和第 II 类错误）以及 P- 值的定义和应用。然后详细阐述了单个正态总体的假设检验问题，包括双边检验、左边检验和右边检验的拒绝域和 P- 值计算。最后探讨了区间估计与假设检验的关系，说明了它们之间的相互转换，以及单侧置信限与单边假设检验的对应关系。（由 claude-3.5-sonnet 生成摘要）

1. 假设检验

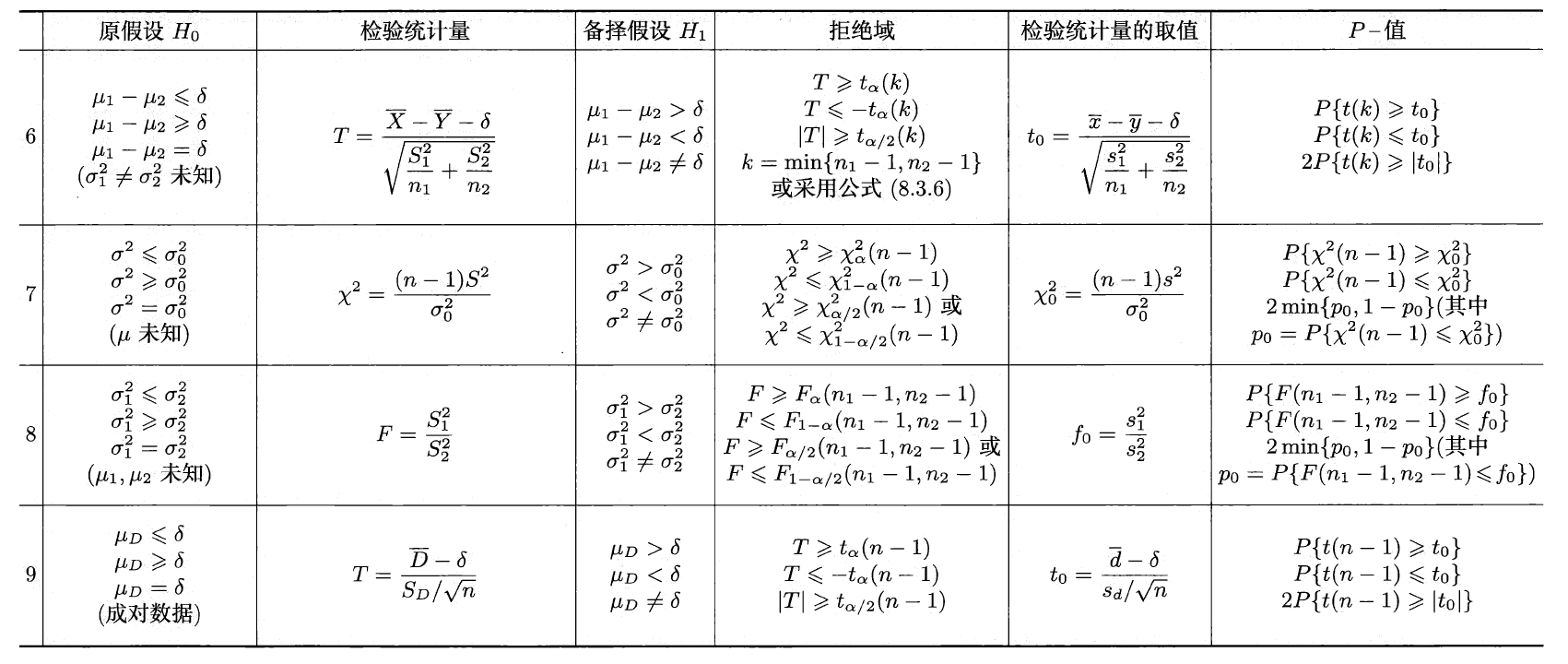
后面假设检验的拒绝域和 P−P_{-} 值都是可以通过检验统计量本身的性质而得到的。故其实第七章和第八章的内容只要背了枢轴量都可以自己推出来。

  • 两类错误
    • (第 I 类错误) 拒绝真实的原假设（弃真）
      • α=P{第 I 类错误}=P{拒绝 H0∣H0 为真}\alpha=P\{ \text{第 I 类错误} \}=P\{ \text{拒绝 }H_{0} \mid H_{0}\text{ 为真} \}
      • 一般来说都是题目中给出，即问你是否有 95%95\% 的把握拒绝原假设，就是问犯第一类错误的概率是否小于 0.05%0.05\%。
    • (第 II 类错误) 接受错误的原假设（取伪）
      • β=P{第 II 类错误}=P{接受 H0∣H0 为假}\beta=P\{ \text{第 II 类错误} \}=P \{ \text{接受 }H_{0} \mid H_{0} \text{ 为假} \}
      • 此类问题需要给出待估参数的真实值，然后根据枢轴量进行计算，具体可参考作业题。
  • (P−P_- 值) 当原假设成立时，检验统计量取比观察到的结果更为极端的数值的概率。
    • 当 P−≤αP_{-} \leq \alpha 时，拒绝原假设；当 P−>αP_{-} > \alpha 时，接受原假设。
    • 双边检验问题中的 P−P_{-} 值可以如下计算：先算出一边的概率 pp，则 P−=2min⁡{p,1−p}P_{-} = 2 \min \{ p,1-p \}。
  • 假设问题与检验（这里以单个正态总体的 ZZ 检验为例）
    • 双边假设问题：H0:μ=μ0,H1:μ≠μ0H_0:\mu=\mu_0,H_1:\mu\neq\mu_0,其中 μ0\mu_0 是已知的常数，由前一节讨论知，可取检验统计量为 Z=Xˉ−μ0σ/nZ=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}
      • 根据 Neyman-Pearson 原则，拒绝域为 W={∣Z∣=∣X‾−μ0σ/n∣≥zα/2}W=\left\{|Z|=\left|\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\right|\geq z_{\alpha/2}\right\}
      • P−=PH0{∣Z∣≥∣z0∣}=2PH0{Z≥∣z0∣}=2(1−Φ(∣z0∣))P_-=P_{H_0}\left\{| Z|\geq| z_0|\right\}=2P_{H_0}\left\{Z\geq| z_0|\right\}=2(1-\Phi(| z_0|))（其中 z0=x‾−μ0σ/nz_0 = \frac{\overline{x}-\mu_0}{\sigma / \sqrt n}）
    • 左边假设问题：H0:μ≥μ0,H1:μ<μ0H_0:\mu\geq \mu_0,H_1: \mu< \mu_0,其中 μ0\mu_0 是已知的常数检验统计量仍取为 Z=Xˉ−μ0σ/nZ=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}. 拒绝域形式为 Z=X‾−μ0σ/n≤C.Z=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\leq C.
      • 根据 Neyman-Pearson 原则，拒绝域为 W={Z=X‾−μ0σ/n≤−zα}W=\left\{Z=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\leq-z_\alpha\right\}
      • P_=Φ(z0)P\_ = \Phi(z_0)
    • 右边假设问题：H0:μ≤μ0,H1:μ>μ0H_0:\mu\leq\mu_0,H_1:\mu>\mu_0, 其中 μ0\mu_0 是已知的常数。检验统计量仍取为 Z=Xˉ−μ0σ/nZ=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}.
      • 根据 Neyman-Pearson 原则，拒绝域为 W={Z=X‾−μ0σ/n≥zα}W=\left\{Z=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\geq z_\alpha\right\}
      • P_=1−Φ(z0)P\_ = 1-\Phi(z_0)

2. 区间估计

  • 两者可以互相转换。例如，μ\mu 的置信水平为 1−α1-\alpha 的置信区间为 X‾−σnzα/2<μ<X‾+σnzα/2\overline{X}-\frac\sigma{\sqrt{n}}z_{\alpha/2}<\mu<\overline{X}+\frac\sigma{\sqrt{n}}z_{\alpha/2}，则假设检验问题 H0:μ=μ0H1:μ≠μ0,H_0:\mu=\mu_0H_1:\mu\neq\mu_0, 的接受域为 W‾={X‾−σnzα/2<μ0<X‾+σnzα/2}\overline{W}=\left\{\overline{X}-\frac{\sigma}{\sqrt{n}}z_{\alpha/2}<\mu_0<\overline{X}+\frac{\sigma}{\sqrt{n}}z_{\alpha/2}\right\}。
  • 一般地，若假设检验问题 H0:θ=θ0H1:θ≠θ0H_0: \theta = \theta _0H_1: \theta \neq \theta _0 的显著水平为 α\alpha 的接受域能等价地写成 θ^L<θ0<θ^U\hat{\theta}_L<\theta_0<\hat{\theta}_U，那么(θ^L,θ^U)\hat{\theta}_L,\hat{\theta}_U) 是参数 θ\theta 的置信水平为 1−α1-\alpha 的置信区间。
    • 反之，若 (θ^L,θ^U\hat{\theta}_L,\hat{\theta}_U) 是 θ\theta 的置信水平为 1−α1-\alpha 的置信区间，则当 θ0∈(θ^L,θ^U)\theta_0\in(\begin{array}{c}\hat{\theta}_L,&\hat{\theta}_U\end{array}) 时，接受双边检验 H0:θ=θ0H_0: \theta = \theta _0, H1:θ≠θ0H_1: \theta \neq \theta _0 中的原假设 H0H_0, 且检验的拒绝域为 θ0≤θ^L\theta _0\leq \hat{\theta } _L 或θ0≥θ^U\theta_0\geq\hat{\theta}_U。
  • 单侧置信限与单边假设检验的关系：
    • 若 θ^L\hat{\theta}_L 是 θ\theta 的置信水平为 1−α1-\alpha 的单侧置信下限，则当 θ0≥θ^L\theta_0\geq\hat{\theta}_L 时，接受右边检验 H0:θ≤θ0H_0: \theta \leq \theta _0, H1:θ>θ0H_1: \theta > \theta _0 中的原假设 H0H_0, 反之，拒绝原假设。
    • 若 θ^U\hat{\theta}_U 是 θ\theta 的置信水平为 1−α1-\alpha 的单侧置信上限，则当 θ0≤θ^U\theta_0\leq\hat{\theta}_U 时，接受左边检验 H0:θ≥θ0H_0: \theta \geq \theta _0, H1:θ<θ0H_1: \theta < \theta _0 中的原假设 H0H_0, 反之，拒绝原假设。

评论

TABLE OF CONTENTS

1. 假设检验
2. 区间估计