VIII. 光学
本篇笔记主要介绍了光学的三个重要章节:光的干涉、光的衍射和光的偏振。在光的干涉部分,详细讨论了光源的基本概念、折射率、光程等基础知识,以及杨氏双缝实验、洛埃镜实验和薄膜干涉等典型实验。在光的衍射部分,介绍了惠更斯原理,并对单缝衍射和光栅衍射进行了深入分析。最后在光的偏振部分,讨论了不同类型的光束、偏振片的原理,以及马吕斯定律和布儒斯特定律等重要规律。(由 claude-3.5-sonnet 生成摘要)
1. Ch20 光的干涉
1.1. 光的基本概念
- 光源:能够发射光波的物体称为光源。
- 热辐射光源:将热能转化为辐射。
- 冷光源:与周围温度相同,不需要加热。
- 普通光源:激发态原子的自发辐射,频率、相位、振动方向或传播方向不相同;谱线宽度 Δλ:10−3∼10−1 nm。
- 激光光源:原子的受激辐射,频率、相位、振动方向和传播方向都相同;谱线宽度 Δλ:10−9 nm。
- 单色光与复色光
- 单色光:具有单一频率的光波。
- 复色光:不同频率单色光的混合光。
- 光强:
- 谱线宽度 Δλ:谱线在光强 I0/2 处的波长范围。
- 折射率:同频率的光波在不同介质中,其波速和波长不一样。
- 设光在真空中的波速为 c0,则在 折射率 为 n 的介质中的波速 c 满足 n=cc0。
- 设光在真空中的波长为 λ,则在 折射率 为 n 的介质中的波长 λn=νc=nλ。
- 光程:光在折射率为 n 的介质中经过的路程为 r 时,称 L=nr 为光程。
- 这是为了方便计算光的相位变化所定义的概念,因为经过光程为 L 所引起的相位差变化为:Δφ=2πλnr=λ2πnr=λ2πL(λ:真空中的波长)。
- 等光程性:光线通过透镜会改变它的传播方向,但不产生附加的光程差。即,物点与象点之间各光线的光程都相等,观测仪器不会带来附加的光程差。
- 半波损失:如果光是从光束介质传向光密介质,则在其分界面上反射时将发生 半波损失,即相位有 π 的突变。折射波没有半波损失。
1.2. 光的干涉
 设符合相干条件的两光矢量 E1,E2 在其原点有:
设符合相干条件的两光矢量 E1,E2 在其原点有:
E1E2=E10cos(ωt+φ10)=E20cos(ωt+φ20)
则在 P 点:
E1=E10cos(ωt−2πn1r1/λ+φ10)E2=E20cos(ωt−2πn2r2/λ+φ20)(2πniri/λ (i=1,2): 从光源 S 到 P 的相位变化量)
矢量合成的结果为:
E02=E102+E202+2E10E20cosΔφΔφ=(φ20−φ10)−λ2π(n2r2−n1r1)
则光发生干涉的判据为:
Δφ={±2kπ,±(2k+1)π,k=0,1,2,… (干涉加强)k=0,1,2,… (干涉减弱)
当 φ10=φ20 时,用 δ=n2r2−n1r1=L2−L1 来表示光程差,则有
δ={±(2k)2λ,±(2k+1)2λ,k=0,1,2,... (干涉加强)k=0,1,2,... (干涉减弱)
- 光的干涉条件:频率相同、振动方向相同、相位差恒定。
- 相干光的获得方法
- 分波阵面法:同一波阵面的不同部分分离出两束相干光。
- 分振幅法:反射光和折射光作为两束相干光。
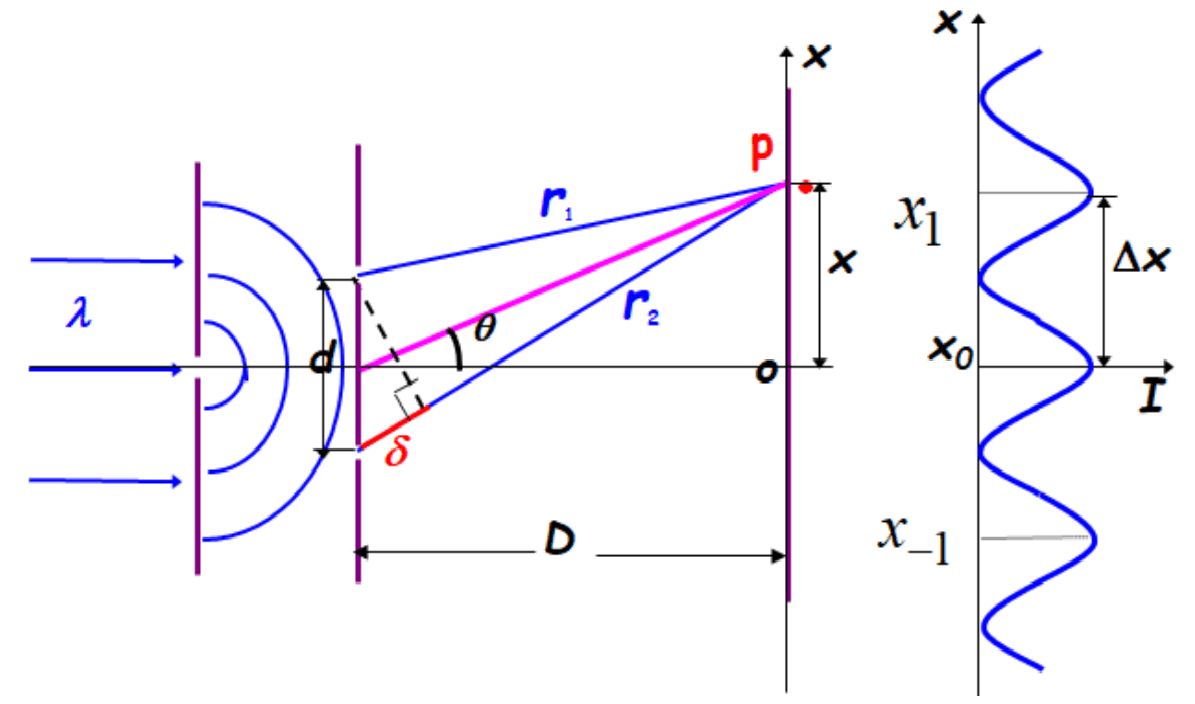 杨氏双缝实验(利用分波阵面法获得相干光)
杨氏双缝实验(利用分波阵面法获得相干光)
- 一般认为实验在真空(或空气)中进行,则光程差为:δ=r2−r1≈dsinθ≈dtanθ=d⋅Dx。
- 相邻两明纹(或暗纹)的间距,实际上就是光程差改变 λ 的位置,有 Δx=dDλ。
- 屏中心处由于 δ=r2−r1=0,是相长干涉,称为 中央亮纹,故有:明条纹 x±k=±kdDλ,暗条纹 x±k=±(2k+1)2dDλ。
- 推论:Δx∝λ,故复色光做实验时,红光在外,紫光在内。
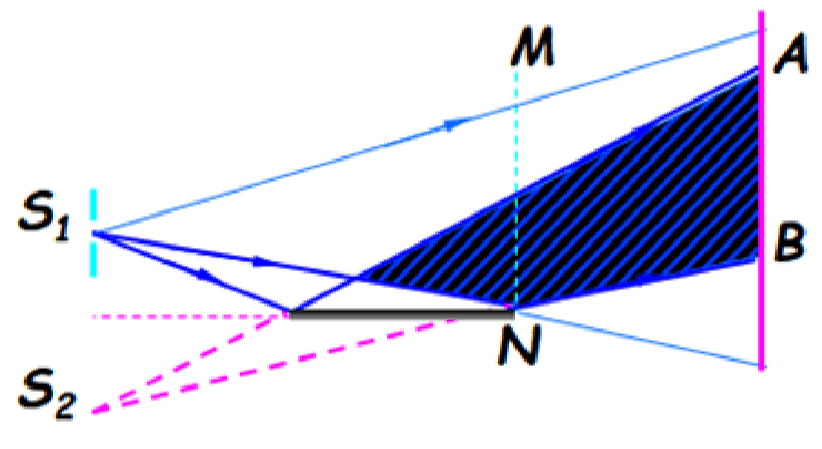 洛埃镜实验(也是利用分波阵面法获得相干光)
洛埃镜实验(也是利用分波阵面法获得相干光)
- 将屏幕移至 NM 的位置,两光束到 N 点的几何路径相同位相差为零,但在 N 处出现的是暗点,这说明反射光有 半波损失。
- 薄膜干涉
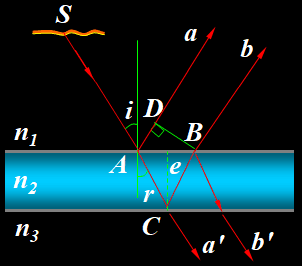 等倾干涉(厚度均匀的薄膜产生的干涉)
等倾干涉(厚度均匀的薄膜产生的干涉)
- 单色光照射到平行的平面薄膜上,在 A 点产生反射和折射,形成 a,b 两光束,其光程差为:δ=n2(AC+CB)−n1AD+δ′。
- 其中 δ′ 是半波损失产生的附加光程差:
- 当 n1>n2>n3 或 n1<n2<n3 时,δ′=0;
- 当 n1<n2>n3 或 n1>n2<n3 时,δ′=2λ。
- 推论:当光垂直入射时,光程差为:δ=2n2e+δ′。
- 等厚干涉(厚度不均匀的薄膜产生的干涉)
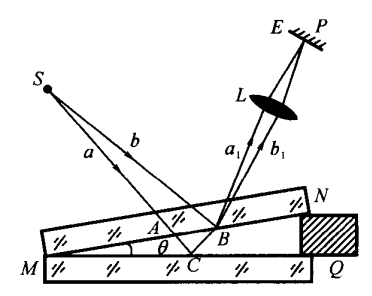 劈尖膜干涉:
劈尖膜干涉:
- 设 n 为中间介质折射率,e 为该位置薄膜厚度,则光程差为:δ=2ne+2λ(两束反射光应刚好一个有半波损失另一个没有)。
- 相邻两明纹(或暗纹)之间的距离为 l=2nsinθλ,与膜的厚度 e 无关。
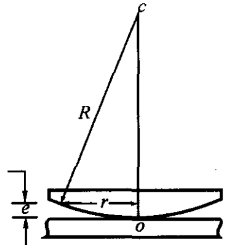 牛顿环:
牛顿环:
- 同理,设对应位置的厚度为 e,则光程差也是:δ=2ne+2λ。
- 设半径为 r,曲率半径为 R,则对应厚度可以用 e≈2Rr2 近似计算。
- 代入解得 k 级明环半径为 rk=(k−21)Rλ,k 级暗环半径为 rk=kRλ,注意牛顿环中间是一个暗斑。
- 光的干涉的应用(注意判断半波损失)
- 增透膜:利用薄膜干涉使反射光减小。
- 高反射膜:利用薄膜干涉折射光减小。
2. Ch21 光的衍射
- 光的衍射现象:光在传播过程中,绕过障碍物而偏离了直线传播的现象。
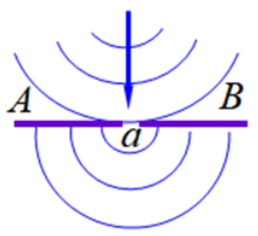 惠更斯原理:媒质中波源 S 所到达的任一点都可以看作一个新的子波源;这些子波源向空间发射球面子波,在以后的任一时刻,这些子波的包络面就是波在该时刻的新的波阵面。——解决了波的传播方向问题
惠更斯原理:媒质中波源 S 所到达的任一点都可以看作一个新的子波源;这些子波源向空间发射球面子波,在以后的任一时刻,这些子波的包络面就是波在该时刻的新的波阵面。——解决了波的传播方向问题- 光的衍射的分类
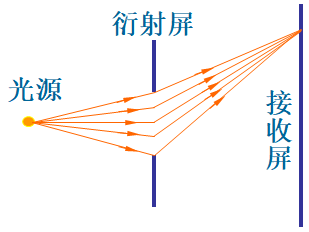 菲涅尔(近场)衍射:是指当光源和接收屏离障碍物(衍射屏)的距离为有限远时,或两者之一离衍射屏的距离为有限远时,所发生的衍射现象。
菲涅尔(近场)衍射:是指当光源和接收屏离障碍物(衍射屏)的距离为有限远时,或两者之一离衍射屏的距离为有限远时,所发生的衍射现象。- 夫琅禾费(远场)衍射:是指衍射屏离光源和接收屏无限远的衍射,相当于入射光和衍射光都为平行光。实验上可利用两个透镜来实现。

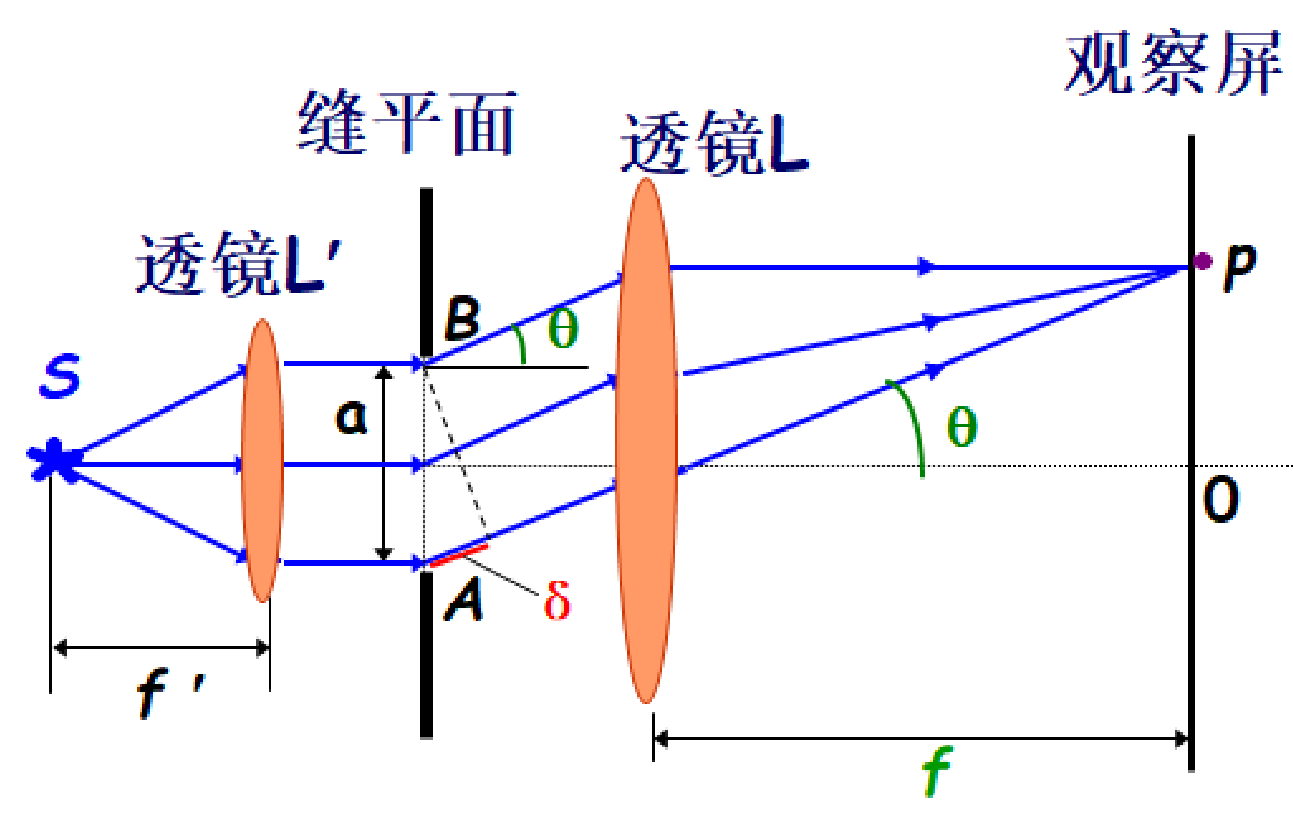 单缝衍射:设平行光垂直入射单缝(如果不是垂直入射,而是存在入射角 i,则将下面的 sinθ 替换为 sinθ+sini)。
单缝衍射:设平行光垂直入射单缝(如果不是垂直入射,而是存在入射角 i,则将下面的 sinθ 替换为 sinθ+sini)。
- 当 θ 不大时,sinθ≈tanθ=fx。
- 单个半波带宽度为 2λ。
- 明暗条纹
- 中央明纹中心:θ=0,注意宽度是其他明纹的两倍。
- 暗纹中心:asinθ=±kλ,k=1,2,⋯
- 明纹中心:asinθ=±(2k+1)2λ,k=1,2,⋯
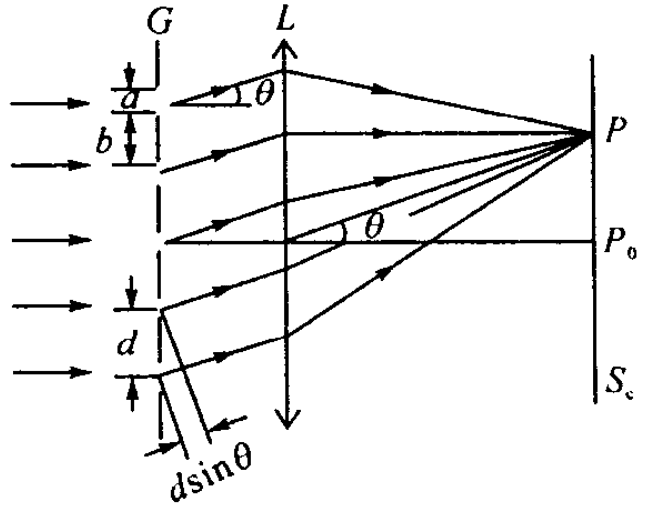 光栅衍射:
光栅衍射:
- 光栅常数 d=a+b,其中 a 为透光缝的宽度,b 为不透光裂痕的宽度。
- 主极大明纹:dsinθ=±kλ, k=0,1,2,⋯ 满足该方程的 θ 初可以看到明纹。由于 −2π<θ<2π,主极大明纹的个数是有限的。
- 缺级:某些衍射角 θ 同时满足光栅方程和单缝衍射的暗纹条件吗,此时原定的主极大明纹就会变成暗纹:{asinθ=k1λ(单缝衍射暗纹)dsinθ=k2λ(光栅主极大)⟹k2=adk1。
- 光栅分辨本领 R=Δλλ=kN。TBD。
3. Ch22 光的偏振
- 光束的分类
- 线偏振光:空间各点的光矢量都沿同一个固定的方向振动。
- 自然光:两个振动方向互相垂直、相位差随机、等振幅的线偏振光组合。
- 部分偏振光:介于自然光和线偏振光之间,振动在各个方向上的振幅不同。
- 偏振片:(理想偏振片)平行于指定方向的振动分量完全通过,垂直于指定方向的振动分量完全吸收。
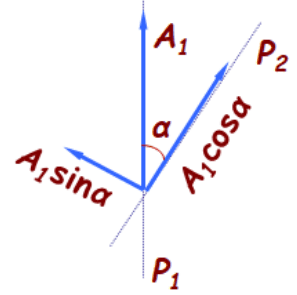 马吕斯定律:设起偏器和检偏器的偏振化方向成 α 角,入射到检偏器的光强为 I1,透射光强为 I2,则 I=I0cos2α。
马吕斯定律:设起偏器和检偏器的偏振化方向成 α 角,入射到检偏器的光强为 I1,透射光强为 I2,则 I=I0cos2α。
- 当 α=0 时 I=Imax=I0;当 α=2π 时,I=0。
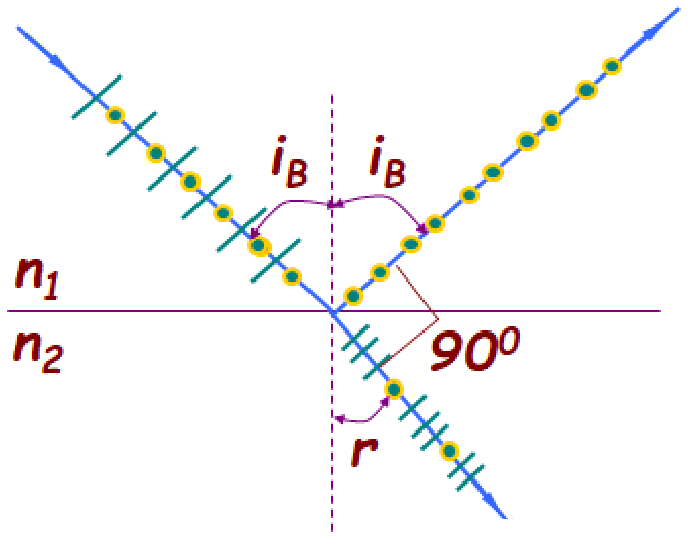 布儒斯特定律:当光线以 iB (称为 布儒斯特角)入射并且满足 iB+r=90° 时,反射光线是完全偏振光,而折射光线仍是部分偏振光,且 taniB=n1n2=n21。
布儒斯特定律:当光线以 iB (称为 布儒斯特角)入射并且满足 iB+r=90° 时,反射光线是完全偏振光,而折射光线仍是部分偏振光,且 taniB=n1n2=n21。
设符合相干条件的两光矢量 在其原点有:
 杨氏双缝实验(利用分波阵面法获得相干光)
杨氏双缝实验(利用分波阵面法获得相干光)
 洛埃镜实验(也是利用分波阵面法获得相干光)
洛埃镜实验(也是利用分波阵面法获得相干光)
 等倾干涉(厚度均匀的薄膜产生的干涉)
等倾干涉(厚度均匀的薄膜产生的干涉)
 劈尖膜干涉:
劈尖膜干涉:
 牛顿环:
牛顿环:
 惠更斯原理:媒质中波源 所到达的任一点都可以看作一个新的子波源;这些子波源向空间发射球面子波,在以后的任一时刻,这些子波的包络面就是波在该时刻的新的波阵面。——解决了波的传播方向问题
惠更斯原理:媒质中波源 所到达的任一点都可以看作一个新的子波源;这些子波源向空间发射球面子波,在以后的任一时刻,这些子波的包络面就是波在该时刻的新的波阵面。——解决了波的传播方向问题 菲涅尔(近场)衍射:是指当光源和接收屏离障碍物(衍射屏)的距离为有限远时,或两者之一离衍射屏的距离为有限远时,所发生的衍射现象。
菲涅尔(近场)衍射:是指当光源和接收屏离障碍物(衍射屏)的距离为有限远时,或两者之一离衍射屏的距离为有限远时,所发生的衍射现象。
 单缝衍射:设平行光垂直入射单缝(如果不是垂直入射,而是存在入射角 ,则将下面的 替换为 )。
单缝衍射:设平行光垂直入射单缝(如果不是垂直入射,而是存在入射角 ,则将下面的 替换为 )。
 光栅衍射:
光栅衍射:
 马吕斯定律:设起偏器和检偏器的偏振化方向成 角,入射到检偏器的光强为 ,透射光强为 ,则 。
马吕斯定律:设起偏器和检偏器的偏振化方向成 角,入射到检偏器的光强为 ,透射光强为 ,则 。
 布儒斯特定律:当光线以 (称为 布儒斯特角)入射并且满足 时,反射光线是完全偏振光,而折射光线仍是部分偏振光,且 。
布儒斯特定律:当光线以 (称为 布儒斯特角)入射并且满足 时,反射光线是完全偏振光,而折射光线仍是部分偏振光,且 。