本篇笔记介绍了静磁学的基本概念和定律。首先讨论了电流的基本性质，包括电流强度、电流密度和稳恒电流的概念，以及电动势和欧姆定律。随后详细阐述了磁场的产生和特性，重点介绍了毕奥-萨伐尔定律，并分析了多种载流导体（直导线、圆线圈、螺线管等）产生的磁场分布。同时还讨论了运动电荷产生的磁场，以及磁场的安培环路定理及其应用。（由 claude-3.5-sonnet 生成摘要）

1. Ch15 电流·磁场

1.1. 电流·电动势

电荷的定向移动形成电流。而电荷的移动需要有能移动的带电粒子，被成为载流子，主要是电子或离子。这个定向移动的速度和无规则运动的速度不同，被称为漂移速度，其数量级为  $10^{-3} \text{ m}\cdot \text{s}^{-1}$。

• 电流强度：单位时间内通过某一截面的电量，$\color{blue} I=\dfrac{\text{d}q}{\text{d}t}$，是标量。
  • 设电流元 $I \text{d}l$ 的横截面积为 $S$，单位时间内有 $n$ 个定向运动的正电荷，带电量 $q$，速度 $v$，则 $I=qnvS$。
• 电流密度：单位时间内通过单位界面的电量：$j=\dfrac{\text{d}I}{\text{d}S_{\perp}}$，$\boldsymbol{j}$ 的方向为正电荷载流子的方向。
  • $\boldsymbol{j}$ 构成了一个矢量场，可以通过 $\color{blue} \boldsymbol{I}=\displaystyle{\int_{S} \boldsymbol{j}\cdot \text{d}\boldsymbol{S}}$ 求得通过导体任意截面的电流强度。
• 稳恒电流：导体中各点电流密度矢量 $\boldsymbol{j}$ 或通过导体任一截面的电流强度 $I$ 不随时间变化的电流。

在导体中的静电平衡一章中我们看到，如果不维持使得载流子运动的电场，电流很快就会消失。这里也有电阻生热的原因。此时，为了维持电流，需要将导体上电势能较低点的载流子搬到较高的地方。对于稳定电流，其电场不变，是静电场，有环路积分为 $0$。故需要非静电力做功。这一非静电力通常用电动势衡量。

• 电动势：电荷 $q$ 受非静电力做功 $W$ 和 $q$ 的比值，即 $\displaystyle{\mathcal{E}=\dfrac{W_{AB}}{q}=\oint_{A}^{B} \boldsymbol{E}_{k} \cdot \text{d}\boldsymbol{l}}$。
  • 电动势与电势的量纲一致，但是物理意义不同，不能等同看待。
• 欧姆定律：$I=\dfrac{U}{R}$。
• 电阻：$R=\rho \dfrac{l}{S}$，电阻率 $\rho$，电导率 $\gamma=\dfrac{1}{\rho}$。
  • 电流密度等于电导率乘以电场强度。

1.2. 磁力·磁场

• 磁感应强度：定义式 $B=\dfrac{F_{\text{max}}}{qv}$，方向沿 $\boldsymbol{F}_{\text{m}} \times \boldsymbol{v}$ 的方向，可通过右手螺旋法则确定。单位 $\text{T}$（特斯拉），$1\text{ T} = 1 \text{ N} \cdot (\text{A} \cdot \text{m})^{-1}$。
• 电流产生的磁场（毕奥-萨伐尔定律）：电流源 $I\text{d}\boldsymbol{l}$ 在点 $P$ 产生的磁场为：$\color{blue}\text{d}\boldsymbol{B}=\displaystyle{\dfrac{\mu_{0}}{4\pi} \frac{I\text{d}\boldsymbol{l} \times \hat{r}}{r^{2}}}$，这里 $\boldsymbol{r}$ 为电流元指向 $P$ 的矢量。
  • $\mu_{0}=4 \pi \times 10^{-7} \text{ N/A}^2$ 为真空磁导率。
  • 右手螺旋定则：
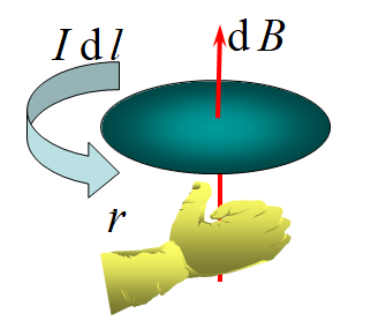
    • 若是直线电流产生的磁场，大拇指指向电流方向，则其它四指的绕行方向就是 $B$ 的方向。
    • 若是环形电流产生的磁场，其它四指的绕行方向为电流方向，则大拇指指向 $B$ 的方向。
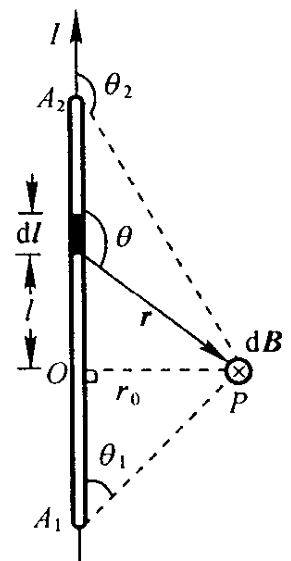  • 载流直导线的磁场：其中任意电流元 $I\text{d}\boldsymbol{l}$ 在同一点 $P$ 处产生的元磁场 $\text{d}\boldsymbol{B}$ 的方向都相同，故总磁感应强度大小为每一微元的代数和：$\color{blue}B=\displaystyle{\dfrac{\mu_{0}}{4\pi} \int_{A_{1}}^{A_{2}} \dfrac{I \text{d} l \sin \theta}{r^{2}} = \dfrac{\mu_{0}}{4\pi} \dfrac{I}{r_{0}} \left( \cos \theta_{1} - \cos \theta_{2} \right)}$。
    • 对于无限长导线，可认为 $\theta_{1}=0$，$\theta_{2} =\pi$，则 $B=\dfrac{\mu_{0}I}{2 \pi r_{0}}$。
    • 对于无限长直导线端点所在垂直平面内，可认为 $\theta_{1}=\dfrac{\pi}{2}$，$\theta_{2}=\pi$，则 $B=\dfrac{\mu_{0}I}{4\pi r_{0}}$。
    • 对于载流直导线延长线上的一点，$B=0$。
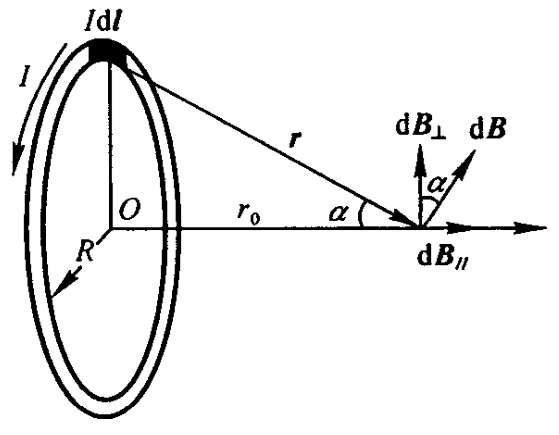  • 载流圆线圈轴线上的磁场：任意电流元在轴线上同一点 $P$ 上产生的元磁场大小相等，但是方向各不相同，其中垂直于轴线的分量相互抵消，只剩下沿轴线的分量：$\displaystyle{B=\oint \text{d}B \sin \alpha =\dfrac{\mu_{0}}{4\pi} \dfrac{I\sin \alpha}{R^{2}+x^{2}}\oint \text{d}l = \dfrac{\mu_{0}IR^{2}}{2(R^{2}+x^{2})^{3/2}}}$。
    • 在圆线圈中心处，$x=0$，则 $B=\dfrac{\mu_{0}I}{2R}$。
      • 在角度为 $\theta$ 的圆弧电流中心处，$B=\dfrac{\mu_{0} I}{2 R} \dfrac{\theta}{2\pi}$。
    • 在轴线上远离圆线圈处，$r_{0} \gg R$，则 $B=\dfrac{\mu_{0}}{2\pi} \dfrac{IS}{x^{3}}$。
      • 引入磁矩 $\boldsymbol{p}_{m}=IS \boldsymbol{e}_{n}$，则有 $B=\dfrac{\mu_{0}}{2\pi} \dfrac{\boldsymbol{p}_{m}}{x^{3}}$。
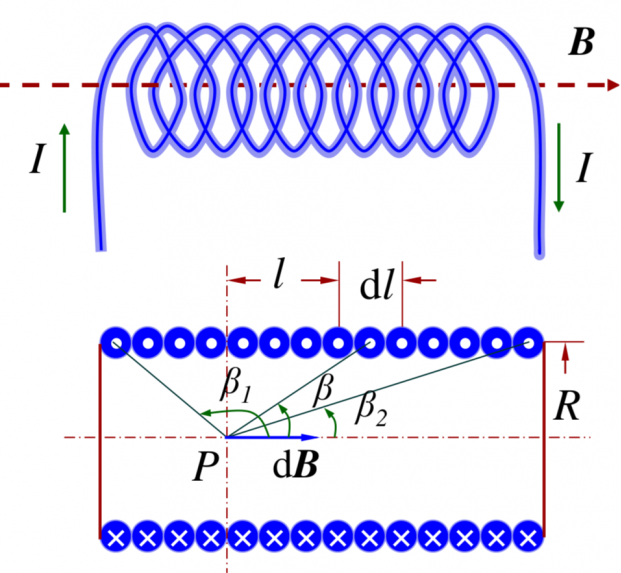  • 载流直螺线管内部的磁场（推荐用安培环路定理分析）：在螺线管上取 $\text{d}l$，相当于电流强度为 $In\text{d}l$ 的圆电流，故 $\displaystyle{\boldsymbol{B}=\int \dfrac{\mu_{0} IR^{2} n \text{ d}l}{2 (R^{2}+l^{2})^{3/2}} = \int_{\beta_{1}}^{\beta_{2}} -\dfrac{\mu_{0}}{2} nI \sin \beta \text{d} \beta} = \dfrac{\mu_{0}}{2} n I \left( \cos \beta_{2} - \cos \beta_{1} \right)$。
    • 当 $L\gg R$ 时，$\beta_{1}\to\pi$，$\beta_{2}\to0$，则 $B=\mu_{0} nI$。
    • 在长直螺线管两端点处，$\beta_{1}\to \dfrac{\pi}{2}$，$\beta_{2}\to\pi$，则 $B=\dfrac{1}{2} \mu_{0} n I$。
• 电荷产生的磁场：以速度 $\boldsymbol{v}$ 运动电荷 $q$ 产生的磁场为：$\color{blue}\boldsymbol{B}=\dfrac{\mu_{0}}{4\pi} \dfrac{q(\boldsymbol{v}\times \hat{r})}{r^{2}}$。
  • 电荷运动的等效电流：在有多电荷（尤其是连续分布电荷）进行匀速运动时，可考察某截面单位时间内通过的电荷量而求等效电流 $I$。
    • 在 $v\ll c$ 的情况下，恒速运动的点电荷产生的电场可认为和该点的静止电荷的静电场没有区别，即 $\boldsymbol{E}=\dfrac{1}{4\pi \epsilon_{0}} \dfrac{q}{r^{2}} \hat{r}$。
• 磁场的安培环路定理：在磁场中，沿任意闭合曲线的磁感应强度的线积分等于真空磁导率 $\mu_{0}$ 乘以穿过该环路所有电流的代数和：$\color{blue}\displaystyle{\oint_{L} \boldsymbol{B} \cdot \text{ d} \boldsymbol{l} = \mu_{0} \sum_{S_{L}} I_{内}}$。
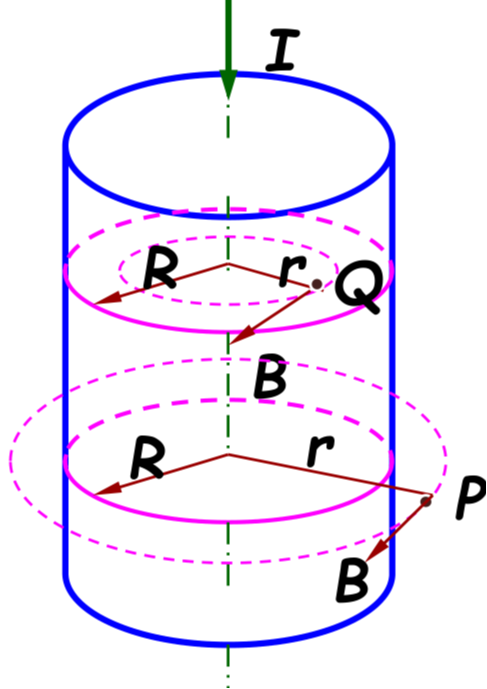  • 无限长载流圆柱体内外的磁场：设圆柱截面半径为 $R$，取距离轴为 $r$ 的一点考察磁场 $B$，沿半径为 $r$ 的圆一周的磁感应强度环积分（即绕磁感应线一周）为 $\displaystyle{\oint_{L} B \text{d} l = B \cdot 2 \pi r}$。
    • 当 $r>R$ 时：$B=\dfrac{\mu_{0}}{2\pi} \dfrac{I}{r}$。
    • 当 $r<R$ 时：
      • 若为电流面（电流仅分布在导体表面）分布，则 $B\cdot 2 \pi r=0$ 即 $B=0$；
      • 若为电流体分布（电流均匀分布在整个导体中），则 $B \cdot 2 \pi r=\mu_{0} I \dfrac{\pi r^{2}}{\pi R^{2}}$，故 $B=\dfrac{\mu_{0}}{2\pi} \dfrac{Ir}{R^{2}}$。
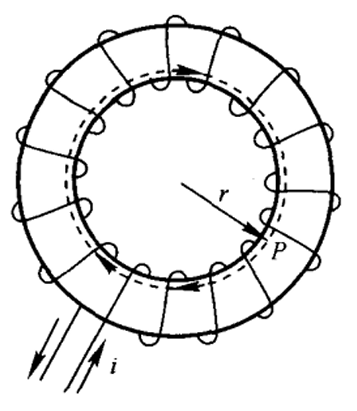  • 载流螺绕环内的磁场：设螺绕环内外径 $r_{1},r_{2}$，总匝数 $N$，电流 $I$。取管内一点 $P$，距离轴线距离 $r\in(r_{1},r_{2})$，则 $\displaystyle{\oint_{L}B \cdot \text{d}l=B\cdot 2\pi r=\mu_{0} NI}$，故 $B=\mu_{0} \dfrac{N}{2R} I$。
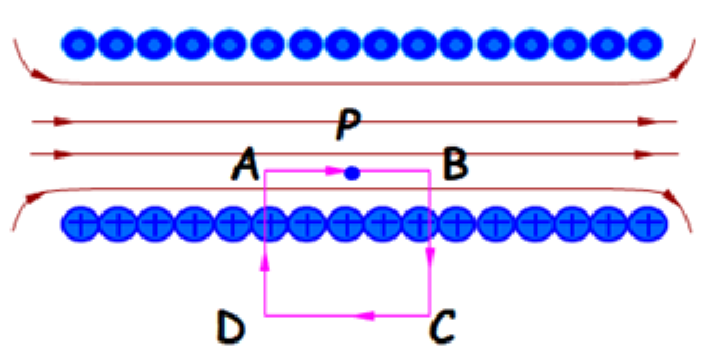  • 载流长直螺线管内的磁场：设螺线管长 $l$，总匝数 $N$，通电流 $I$。取管内一点 $P$，如图作一矩形闭合回路 $ABCDA$，其中 $AD,DC,BC$ 段均有 $B\cdot \text{d}l=0$，故 $\displaystyle{\oint_{L} B\cdot \text{d}l=\int_{AB}B\cdot \text{d}l=B\cdot |AB|}$。考虑被包围的总电流为 $I'=\dfrac{N}{l} I \cdot |AB|$，故 $B=\mu_{0} \dfrac{N}{l} I$。
    • 如果用 $n$ 表示单位长度环绕的线圈匝数，则螺绕环和螺线管的公式都可以统一为 $\color{blue}B=\mu_{0} nI$。
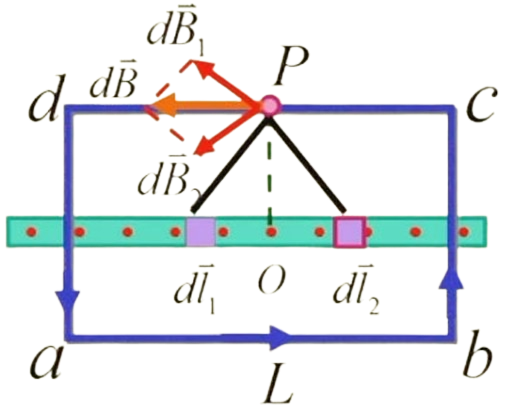  • 无限大载流平面的磁场：$\color{blue}B=\dfrac{\mu_{0}}{2} j$，这里 $j$ 为电流线密度，磁场方向与平面平行，可以通过右手螺旋定则确定。
• 磁通量：类似于引入电通量的方法，定义磁通量为：$\Phi_{B}=\displaystyle{\int_{S}\boldsymbol{B}\cdot \text{d}\boldsymbol{S}}$。
  • 单位为 $\text{Wb}$（韦伯）。
• 磁场的高斯定理：由于自然界不存在磁荷，故任意封闭曲线面的磁通量为 $0$，即 $\displaystyle{\oint_{S}\boldsymbol{B}\cdot \text{d}\boldsymbol{S}=0}$。

1.3. 磁场中的作用力

• 安培力：安培力是洛伦兹力的宏观表现。载流导线（可以等效为从起点到终点的直导线 $\boldsymbol{L}$）在磁场 $\boldsymbol{B}$ 中所受安培力为 $\displaystyle{\color{blue} \boldsymbol{F}=\int_{L} I\text{d} \boldsymbol{l} \times \boldsymbol{B}=I \boldsymbol{L}\times \boldsymbol{B}}$。
  • 两根平行载流直导线的作用力：$F_{m}=\dfrac{\mu_{0}}{2\pi} \dfrac{I_{1}I_{2}}{d}$（$\mu_{0}=2\pi k=4\pi \times 10^{-7} \text{ N} \cdot \text{A}^{-2}$）。
• 磁矩：磁矩是与闭合回路有关的物理量 $\color{blue}\boldsymbol{p}_{m}=NI S\boldsymbol{e}_{n}$，这里 $N$ 是线圈匝数，对于其中任一匝的围成的平面，$S$ 是其面积，$\boldsymbol{e}_{n}$ 是其法向量。
• 载流平面线圈的磁力矩：
  • 均匀磁场对载流线圈的合作用力为 $0$，但存在力矩 $\color{blue}\boldsymbol{M}=\boldsymbol{p}_{m} \times \boldsymbol{B}$。
  • 一般磁场对载流线圈的磁力矩为 $\color{blue}\text{d}\boldsymbol{M}=\boldsymbol{r}\times (I\text{d}\boldsymbol{l} \times \boldsymbol{B})$。

2. Ch16 物质中的磁场

2.1. 磁介质

分子本身具有磁矩（固有磁矩 $\boldsymbol{p}_{m}$），可认为由等效的圆电流（分子电流）产生。由于磁矩取向无规则，它们相互抵消，导致磁介质不显磁性。磁介质处于外磁场时，每个分子均产生与外磁场方向相反的 附加磁矩 $\Delta \boldsymbol{p}_{m}$。顺磁质的 $\boldsymbol{p}_{m}$ 远大于 $\Delta \boldsymbol{p}_{m}$，且分子受到的磁力矩尽可能使固有磁场转向外磁场方向；抗磁质的 $\boldsymbol{p}_{m}$ 为 $0$，附加磁矩是产生磁化的唯一原因。

• 磁介质：在磁场的作用下能够获得磁矩的物质。磁介质内的磁感应强度 $\boldsymbol{B}$ 为真空中原来的磁感应强度 $\boldsymbol{B}_{0}$ 和附加磁感应强度 $\boldsymbol{B}'$ 的和，即 $\boldsymbol{B}=\boldsymbol{B}_{0}+\boldsymbol{B}'$。
• 分子电流：分子或原子中所有电子对外界所产生磁效应总和可以等效于一个圆电流 $I$。
• 分子磁矩：每一个分子电流都具有磁矩，具有关系 $\boldsymbol{p}_{m} = I S \boldsymbol{e}_{n}$。
• 磁化强度：表征磁介质磁化程度。定义为某体积微元内分子的总磁矩之和 $\color{blue}\displaystyle{\boldsymbol{M}=\sum \dfrac{\boldsymbol{p}_{m}}{\text{d}V}}$。
  • 顺磁质 $\boldsymbol{M}$ 与 $\boldsymbol{B}_{0}$ 同向，抗磁质 $\boldsymbol{M}$ 与 $\boldsymbol{B}_{0}$ 反向。
  • 如果介质内各点的 $\boldsymbol{M}$ 都相同，称为均匀磁化，否则称为不均匀磁化。
• 磁化电流 / 束缚电流：由磁介质中各分子的分子电流叠加而成，仅在磁介质表面产生的等效环形电流（或者说是宏观上未被抵消而沿圆柱面流动的电流），常用 $I_{\text{m}}$ 表示。
  • 磁介质表面上某处 磁化电流线密度 $j_{\text{m}}$ 等于该点磁化强度 $\boldsymbol{M}$ 沿表面的切向分量：$\displaystyle{M=\sum \dfrac{p_{m}}{\Delta V}=\dfrac{j_{m}lS}{Sl}=j_{m}}$，其正负可以通过考察是顺磁质还是抗磁质得到。

2.2. 磁场强度

• 磁场强度：定义式：$\color{blue}\boldsymbol{H}=\dfrac{\boldsymbol{B}}{\mu_{0}} - \boldsymbol{M}$，单位 $\text{A/m}$。
  • 束缚电流与磁化强度的关系：介质内 $M=j_{\text{m}}$，磁化强度 $\boldsymbol{M}$ 对闭合回路的线积分等于通过回路所包围的束缚电流，即 $\displaystyle{\oint_{L} \boldsymbol{M}\cdot\text{d}\boldsymbol{l}=j_{\text{m}} |AB|=\sum_{L\text{内}}I_{\text{m}}}$。这虽然是通过均匀磁介质与矩形闭合回路推导出的，但对于任何情况都普遍适用。
• 磁化率：对于各向同性的电介质，$\boldsymbol{M}$ 与 $\boldsymbol{H}$ 成正比：$\color{blue}\boldsymbol{M}=\chi_{m}\boldsymbol{H}$，其中 $\chi_{m}$ 称为磁化率。
  • 对于抗磁质：$\chi_{m}<0$，$\mu_r<1$，$B<B_{0}$。
  • 对于顺磁质：$\chi_{m}>0$，$\mu_{r}>1$，$B>B_{0}$。
  • 对于铁磁质：$\chi_{m}$ 很大且不是常数，$B\gg B_{0}$。
• 相对磁导率：相对磁导率 $\color{blue}\mu_{r}=1+\chi_{m}$，有 $\boldsymbol{B}=\mu_{0}\mu_{r}\boldsymbol{H}=\mu_{0}(1+\chi_{m}) \boldsymbol{H}=\mu_{0}\boldsymbol{H}+\mu_{0}\boldsymbol{M}$。
• 有磁介质时的安培环路定理：$\color{blue}\displaystyle{\oint_{L} \boldsymbol{H}\cdot\text{d}\boldsymbol{l}=\sum I_{0}}$。
  • 有介质时的磁场高斯定理依然成立，即闭合曲线面积分为 $0$。

3. Ch19 带电粒子在电场和磁场中的运动

• 洛伦兹力：速度为 $\boldsymbol{v}$ 的运动电荷在磁感应强度为 $\boldsymbol{B}$ 的某点受到的磁场作用力（洛伦兹力）为 $\boldsymbol{F}=q \boldsymbol{v} \times \boldsymbol{B}$。
  • 若空间中同时存在电场 $E$ 和磁场 $B$，则电荷所受作用力为 $\boldsymbol{F}=q\boldsymbol{E}+q \boldsymbol{v} \times \boldsymbol{B}$。
    • 考虑相对论效应后：$q\boldsymbol{E}+q\boldsymbol{v}\times \boldsymbol{B}=\dfrac{\text{d}}{\text{d} t} \left( \dfrac{m\boldsymbol{v}}{\sqrt{1-(v/c)^{2}}} \right)$。
• 带电粒子在磁场中的运动：
  • $\boldsymbol{v}\parallel \boldsymbol{B}$：带电粒子作匀速直线运动。
  • $\boldsymbol{v}\perp \boldsymbol{B}$：带电粒子作匀速圆周运动，圆周半径 $R=\dfrac{mv}{qB}$，周期 $T=\dfrac{2\pi m}{qB}$。
  • $\boldsymbol{v}$ 与 $\boldsymbol{B}$ 呈任意夹角 $\theta$，则带电粒子作等间距螺旋线运动，运动半径 $R=\dfrac{mv_{\perp}}{qB}=\dfrac{mv \sin \theta}{qB}$，螺距：$h=\dfrac{2\pi m v_{\parallel}}{qB}=\dfrac{2\pi mv \cos \theta}{qB}$。
• 霍尔效应：在磁场中载流导体上出现横向电势差的现象，其霍尔电压为 $V_H=R_{H} \dfrac{IB}{d}$，$d$ 为导体板的厚度。
  • 霍尔系数：$R_{H}=\dfrac{1}{nq}$，若测得 $R_{H}$，就可以求出导体中载流子的浓度。

4. Ch17 电磁感应

• 法拉第电磁感应定律 / 楞次定律：$\mathcal{E}_{i}=- \dfrac{\text{d}\Phi_{B}}{\text{d}t}$。
• 电动势：是指在电源内部，将单位正电荷从负极经电源内部移到正极时非静电力所作的功，$\displaystyle{\mathcal{E}=\dfrac{\text{d} A}{\text{d} q} =\oint_{-}^{+} \boldsymbol{E}_{k} \cdot \text{d} \boldsymbol{l}}$。
• 感生电动势：由于磁场变化而产生的电场称为 涡旋电场，涡旋电场产生的电动势称为感生电动势，$\displaystyle{\color{blue}\mathcal{E}=\oint_{L}\boldsymbol{E}_{\text{旋}} \cdot \text{d}\boldsymbol{l}=-\dfrac{\text{d}\Phi_{B}}{\text{d}t}}$。
  • 半径为 $r$ 的无限长圆柱内沿轴线方向通随时间均匀变化的磁场 $B$，则涡旋电场分布：$E_{旋}=-\dfrac{r}{2} \dfrac{\text{d}B}{\text{d}t},\space r\leq R;\quad E_{旋}=-\dfrac{R^{2}}{2r} \dfrac{\text{d}B}{\text{d}t},\space r\geq R$。其中 $- \dfrac{\text{d}\boldsymbol{B}}{\text{d}t}$ 与 $\boldsymbol{E}_{\text{旋}}$ 在方向上满足右手螺旋定则。
• 楞次定律：感应电流总是使感应电流所激发的磁场去阻止原磁通量的变化。可用于判断感应电流的方向。
• 动生电动势：导体在恒定磁场中运动时产生的感应电动势，$\displaystyle{\mathcal{E}_{ab}= -\dfrac{\text{d} \Phi_{B}}{\text{d} t} = \int_{a}^{b} (\boldsymbol{v} \times \boldsymbol{B})\cdot \text{d}\boldsymbol{l}}$。
  • 若 $\mathcal{E}_{ab}<0$，则 $V_{a}<V_{b}$；若 $\mathcal{E}_{ab}>0$，则 $V_a>V_{b}$。