本篇笔记介绍了静电学的基本概念和定律。首先讨论了电荷的基本性质和库仑定律，引入了电场强度的概念，并阐述了电通量和高斯定理。随后详细探讨了电势和电势能的关系，以及它们与电场的联系。最后分析了导体在静电平衡时的特性，包括导体表面的电荷分布和静电屏蔽现象，并讨论了各种典型带电体（如带电球壳、球体、直线和平面）的电场与电势分布。（由 claude-3.5-sonnet 生成摘要）

1. Ch13 静电场

1.1. 电荷·电场·电场强度

• 电荷量子化：带电粒子的电量只能是基本电荷 $e=1.60217733 \times 10^{-19} \text{ C}$ 的整倍数。
• 库仑定律：$\displaystyle{\color{blue}\boldsymbol{F}_{12} =\dfrac{1}{4\pi \varepsilon_{0} }\frac{q_1q_2}{r^2}\hat{\boldsymbol{r}}_{12} }$。
• 电场强度：单位试验电荷（电量小，可看成点电荷）在该点所受电场力，$\displaystyle{\color{blue}\boldsymbol{E} = \dfrac{\boldsymbol{F}}{q_{0}}} \displaystyle{ = \frac1{4\pi\varepsilon_0}\int\frac{\mathrm{d}q}{r^2}\hat{r}}$（第二个等号为 场强叠加原理）。
  • 线分布：$\text{d}q = \lambda \text{d}l$；面分布：$\text{d} q = \sigma \text{d} s$；体分布：$\text{d}q = \rho \text{d}V$。
• 电通量：$\Phi_E=\displaystyle{\int_{S}\boldsymbol{E}\cdot\text{d}\boldsymbol{S}}$。
• 电通量的高斯定理：$\color{blue}\Phi_{E} = \displaystyle{\oint_{S} \boldsymbol{E} \cdot \text{d}\boldsymbol{S}=\frac{1}{\varepsilon_0}\sum_iq_{i(\text{内})}}$（这里 $S$ 是闭合曲面）；即闭合曲面的电通量等于内部电荷量除以 $\varepsilon_{0}$，一般取 $\boldsymbol{E}$ 与 $\text{d}\boldsymbol{S}$ 同向的情况方便计算。
  • 对于均匀带电球面：对于球面外任一点，有 $\boldsymbol{E}=\dfrac q{4\pi\varepsilon_0r^2}\hat{\boldsymbol{r}}$。
  • 对于轴对称分布（包括无限长均匀带电的直线，圆柱面，圆柱体等）：$E=\dfrac\lambda{2\pi\varepsilon_0r}$。
  • 对于无限大平面电荷（包括无限大的均匀带电平面，平板等）：$E=\dfrac{\sigma}{2\varepsilon_0}$。

1.2. 电势

• 静电场环路定理：对于任意闭合曲线 $L$，有 $\displaystyle{\oint_{L} \boldsymbol{E} \cdot \text{d} \boldsymbol{l} = 0}$。
• 电势能：当试验电荷 $q_{0}$ 从 $a$ 移到 $b$，其间电场力（保守力）所做的功应等于电荷静电势能增量的负值，$\displaystyle{\color{blue}W_{ab}=q_0\int_a^b\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{l}=-(W_{b}-W_{a})=-\Delta W}$。
  • 电荷从高电势能点移向低电势能点，电势能减小，电场力做正功；
    电荷从低电势能点移向高电势能点，电势能增加，电场力做负功。
  • 电势能是相对的，需要规定一个电势能为 $0$ 的参考点。一般选无限远点或接地为 $0$。规定无限远点为 $0$ 时有 $\displaystyle{W_{P} = q_{0} \int_{P}^{\infty} q_{0} \boldsymbol{E} \cdot \text{d}\boldsymbol{l}}$。
  • 对于点电荷电场的情况可以推出 $W_{ab}=\displaystyle{\int_{r_{a}}^{r_{b}} \dfrac{1}{4\pi \epsilon_{0}} \dfrac{q_{0}q}{r^{2}} \text{d}r = \dfrac{q_{0}q}{4\pi \epsilon_{0}} \left( \dfrac{1}{r_{1}}-\dfrac{1}{r_{2}} \right)}$。
• 电势：某点电势能与其电荷量的比值，是只与位置有关的函数，$\color{blue}\displaystyle{U_P=\frac{W_P}{q_0}=\int_P^{P_{0}}\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{l}}$（这里 $P_{0}$ 是势能零点）。
  • 电场和电势的关系：$\boldsymbol{E} = -\nabla \boldsymbol{V}$。
  • 静电力与电势能的关系：$\boldsymbol{F} = -\nabla \boldsymbol{U}$。
  • 点电荷在电场中的电势：$U_{p} = \dfrac{q}{4\pi \varepsilon_{0} r}$。
• 电势差 / 电压：$U_{ab} =\displaystyle{U_a-U_b = \int_{a}^{\infty} \boldsymbol{E} \cdot \text{d}\boldsymbol{l}- \int_{b}^{\infty} \boldsymbol{E} \cdot \text{d}\boldsymbol{l} =\int_a^b\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{l}}$。
  • 沿着电场线方向，电势降低。
• 常见带电体的电场与电势分布：
  • 均匀带电球壳
    • 电场：$E=\begin{cases}0\quad& r <R\\ \dfrac{q}{4 \pi \varepsilon_{0} r^{2}}\quad&r > R\end{cases}$
    • 电势：$U=\begin{cases} \dfrac{q}{4 \pi \varepsilon_{0}R}\quad& r<R\\ \dfrac{q}{4\pi \varepsilon_{0}r}\quad&r>R\end{cases}$
  • 均匀带电球体
    • 电场：$E=\begin{cases} \dfrac{rq}{4 \pi \varepsilon_{0} R^{3}}\quad& r<R\\ \dfrac{q}{4 \pi \varepsilon_{0} r^{2}}\quad& r>R\end{cases}$
  • 均匀无限长带电直线
    • 电场：$E= \dfrac{\lambda}{2\pi \varepsilon_{0} r} = \dfrac{1}{\varepsilon_{0}}\dfrac{\lambda \text{d}l}{2\pi r \cdot \text{d}l}$
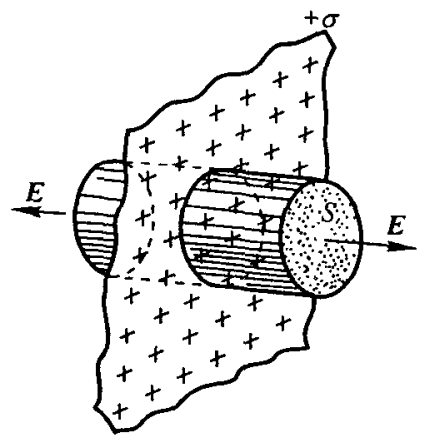
  • 均匀无限大带电平面
    • 电场：$E=\dfrac{\sigma}{2\varepsilon_{0}}=\dfrac{1}{\varepsilon_{0}} \dfrac{\sigma S}{2S}$
      • 推论：无限大平行板电容器内部电场：$E=\dfrac{\sigma}{\varepsilon_{0}}$（在外部来自两块极板的电场相互抵消）

2. Ch14 静电场中的导体和电介质

2.1. 导体

• 静电平衡：外电场引起导体上自由电子的移动，使导体带上等量异号的 感应电荷；感应电荷激发附加电场，改变导体内外的电场。当导体内的外电场与附加电场正好相互抵消时，导体上的自由电子停止宏观运动，导体达到 静电平衡。
  • 导体内部场强处处为零 。
  • 导体是一个等势体，导体表面是一个等势面。
  • 电荷只分布在导体的表面上，所有电荷的代数和等于初始电荷量。
  • 导体表面场强：$E=\dfrac{\sigma}{\varepsilon_{0}}$。
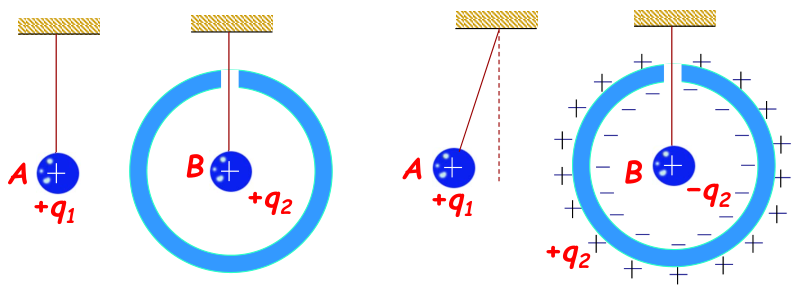
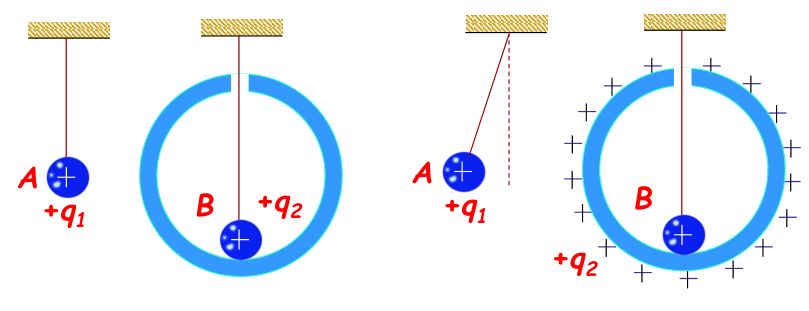
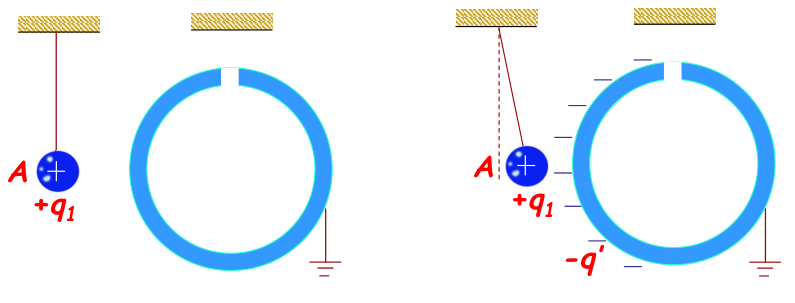
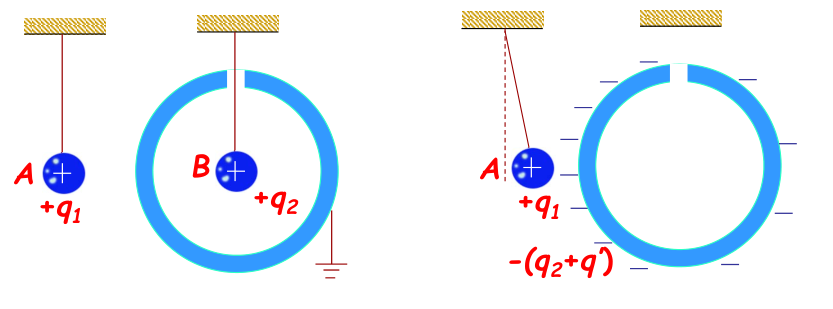
• 静电屏蔽：利用接地空腔导体将腔内带电体与外界隔绝的现象。腔外电场不能穿入腔内，腔内电场恒为零；导体接地可以屏蔽内电场。
  • 应用：高压带电作业，电气设备金属罩接地等。

TBD：补充一下空腔相关的各种分析。

静电场中的导体分析（$+q_1\ll+q_{2}$）

图示	分析
	现感应电荷 $+q_2$，$B$ 球所带电量 $+q_2$ 与球壳内表面所带电量 $-q_2$ 对外产生电场完全抵消，故 $A$ 球受到球壳外表面电荷 $+q_2$ 的斥力。
	在球壳外表面将出现带电量分别为 $+q’$ 和 $-q’$ 的感应电荷。总电荷虽为零，但负电荷靠近 $A$ 球，而正电荷远离 $A$ 球，故 $A$ 球总体上受吸引力。
	$B$ 球与球壳内表面接触，则构成一体，$B$ 球所带的电荷 $+q_2$ 全部转移到了球壳外表面。
	接地球壳电势为零，球壳表面的正感应电荷与大地所带的负电荷中和，只剩负感生电荷 $-q’$。
	内表面出现感应电荷 $-q_2$，由于接地，外表面感应电荷仍为 $-q’$。
	拆地线后，球壳所带总电量为 $-(q_2+q’)$，当 $B$ 球移去后，这些电荷全部跑到外表面，故 $A$ 球受吸引力。

2.2. 电容

• 孤立球导体电容：$\displaystyle{C=\dfrac{q}{U}=4\pi \varepsilon_{0}R}$。
• 电容器的电容：$\color{blue}C=\dfrac{Q}{U_{A}-U_{B}}$（单位为 $\text{F}$）；注意，这里的带电量 $Q$ 是一侧极板带电量的绝对值。
  • 平行板电容器：$C=\dfrac{Q}{U_{A}-U_{B}}=\displaystyle{\dfrac{\varepsilon_{0}S}{d}}$
  • 圆柱形电容器：$\displaystyle{C=\frac{2\pi\varepsilon_0l}{\ln\frac{R_B}{R_A}}}$
  • 球形电容器：$\displaystyle{C=4\pi\varepsilon_0\frac{R_AR_B}{R_B-R_A}}$
• 电容器的串联：总电势差为每个电容器电势差的和，极板电量都相同；$\displaystyle{\frac1C=\frac1{C_1}+\frac1{C_2}+\cdots+\frac1{C_N}}$。
• 电容器的并联：总电量为每个电容器所带电量的和，两板间电势差都相同；$C=C_1+C_2+\cdots+C_N$。
• 电介质充满电容器可增大电容 $\varepsilon_{r}$ 倍，即 $C=\varepsilon_{r} C_0$。

2.3. 电介质的极化

• 电介质：是电的非导体（绝缘介质）。在外电场中时，对电场有影响。处于静电平衡时，内部场强不为零。
• 电介质的极化：电介质在外场中时，在与外电场 $\boldsymbol{E}_{0}$ 垂直的表面层里会出现不能自由移动的正负电荷层，这一现象称为 电介质的极化，这些电荷称为 束缚电荷 或 极化电荷。
• 电介质中的场强：极化电荷会激发电场 $\boldsymbol{E'}$，与自由电荷激发的电场 $\boldsymbol{E}_{0}$ 作矢量和可以得到电介质中的合场强 $\boldsymbol{E}=\boldsymbol{E}_{0}+\boldsymbol{E}'$。
• 极化强度：某点对应的体积微元中所有分子电矩的矢量和 $\boldsymbol{P}$；外加电场不太大时，有线性关系 $\boldsymbol{P}=\varepsilon_{0} \chi_{e} \boldsymbol{E}=\varepsilon_{0} (\varepsilon_{r} - 1) \boldsymbol{E}$。
  • 极化电荷面密度：均匀电介质极化时，电介质表面上某点处的极化电荷面密度 $\sigma'$ 等于极化强度在该点表面的法向分量 $\color{blue}\sigma'=\boldsymbol{P}\cdot \boldsymbol{e}_{n}$。
• 电位移：为了不考虑极化电荷和附加电场，引入电位移 $\color{blue}\boldsymbol{D}=\varepsilon_{0} \boldsymbol{E}+\boldsymbol{P}=\varepsilon_{0} \varepsilon_{r} \boldsymbol{E}=\varepsilon \boldsymbol{E}$。电位移并没有实际物理意义。
• 电介质中的高斯定理：通过电场中任意闭合曲面的位移电通量，等于该闭合面所包围的自由电荷的代数和。$\displaystyle{\oint_{S} \boldsymbol{D} \cdot \text{d} \boldsymbol{S} = \sum q_{0}}$（这里 $S$ 是闭合曲面）。

2.4. 静电场中的能量

• 点电荷系统的能量：$\color{blue}\displaystyle{W=\dfrac{1}{2} \sum q_{i} U_{i}}$，这里 $U_{i}$ 在点电荷 $q_{i}$ 处除了 $q_{i}$ 以外所有电荷产生的电势。
  • 可以通过考虑将每个电荷依次（所以这里会有一个 $1 / 2$ 的系数）移到无穷远处得到。
• 电场能量：定义单位体积上的电场能量为 电能密度 $\color{blue}\omega_{e}=\dfrac{1}{2} \varepsilon E^{2} = \dfrac{1}{2} DE$，则 $\displaystyle{W=\int_{V} \omega_{e} \text{d} V}$。
  • 电容器的能量：$W=\dfrac{1}{2} \dfrac{Q^{2}}{C}$。