II. 刚体力学

2024 年 4 月 24 日

本篇笔记主要介绍了刚体力学的基本概念和定律。首先定义了刚体模型，然后讨论了刚体的质心运动，包括平动、质心坐标和质心运动定理。接着探讨了刚体的定轴转动，介绍了转动平面的概念以及角位移、角速度和角加速度等物理量。最后还提到了匀变速定轴转动的相关公式。这些内容为理解和分析刚体运动提供了基础。（由 claude-3.5-sonnet 生成摘要）

1. Ch6 刚体力学

解题指导

1.1. 刚体模型

刚体：在任何外力作用下，形状和大小均不发生改变的物体。

在外力作用下，任意两点间均不发生位移；
内力无穷大的特殊质点系；
理想模型。

1.2. 刚体的质心运动

刚体的平动：刚体上任意两点的连线始终保持平行的运动。

平动时刚体上各质点的运动相同，因而刚体的平动可用刚体的质心运动描述。

质心：描述刚体整体运动的一个特殊点。

刚体的质心坐标：在直角坐标系中，刚体的质心坐标为：

x_c = \frac{\int x \text dm}{m} \quad y_c = \frac{\int y \text dm}{m} \quad z_c = \frac{\int z \text dm}{m}

质心运动定理： $\boldsymbol{F_\text{外}} = m \boldsymbol{a_c}$ ，这里 $\boldsymbol{F_{\text{外}}}$ 为左右在刚体上的合外力， $\boldsymbol{a_c}$ 为质心加速度。

1.3. 刚体的定轴转动

刚体的定轴转动：刚体中各质点都绕某一直线做圆周运动，这种运动称为定轴转动。

刚体的一般运动可看作平动和转动的合成。

转动平面：刚体内取一点 $P$ ，做转轴的垂足 $O$ ，通过 $OP$ 并与转轴垂直的平面。

刚体绕转轴转动时，质点 $P$ 在转动平面内做圆周运动，可用圆周运动的角量描述。
刚体中任意一点的角位移、角速度、角加速度，可代表整个刚体的角量运动。

角位移： $\text d \boldsymbol{\varphi}$

角速度： $\boldsymbol{\omega} = \dfrac{\text d \boldsymbol{\varphi}}{\text d t}$

角加速度： $\boldsymbol{\beta} = \dfrac{\text d\boldsymbol{\omega}}{\text d t}$

类比于匀速直线运动公式，在匀变速定轴转动中，我们有

\begin{cases} \omega=\omega_0+\beta t \\ \theta = \theta_0 +\omega_0t + \beta t^2 / 2 \\ \omega^2 - \omega_0^2 = 2 \beta (\theta - \theta_0) \end{cases}

1.4. 刚体的转动惯量

转动惯量： $\displaystyle{J = \int r^2 \text dm}$

刚体转动惯量与三个因素有关：刚体的总质量、质量分布、转轴的位置。

对

\text dm

的理解

质量为线分布： $\text dm = \lambda(l) \text dl$
质量为面分布： $\text dm = \sigma(\boldsymbol{r}) \text dS$
质量为体分布： $\text dm = \rho(\boldsymbol{r}) \text d V$

圆盘和圆环的转动惯量

求质量为 $m$ 、半径为 $R$ 的均匀圆环的转动惯量。轴与圆环平面垂直并通过圆心。

J = \int R^2 \text dm = R^2 \int \text dm = m R^2

求质量为 $m$ 、半径为 $R$ 、厚为 $l$ 的均匀圆盘的转动惯量。轴与圆盘平面垂直并通过圆心。

J = \int r^2 \text dm= \int r^2 \rho \cdot 2 \pi r \text d r \cdot l = \int_0^R \rho \cdot 2 \pi l r^3 \text d r = \frac{1}{2} \rho \pi R^4 l

由 $\rho = \dfrac{m}{\pi R^2 l}$ 可得 $J=\dfrac{1}{2} m R^2$ 。

回转半径：回转半径的定义式为 $R_G=\sqrt{\dfrac{J}{m}}$ 。

刚体对轴的角动量： $\boldsymbol{L} = J \boldsymbol{\omega}$ 。

平行轴定理：设两平行轴之间的垂直距离为 $d$ ，有

J = J_c + m d^2

垂直轴定理：设刚体薄板在 $x O y$ 平面内对 $x$ 轴和 $y$ 轴的转动惯量分别为 $J_x$ 和 $J_y$ ，则薄板对 $z$ 轴的转动惯量为：

J_z=J_x+J_y

常见刚体的转动惯量

物体	转动惯量	例图
细杆	垂直于杆、通过杆中心的轴 $J=\dfrac{1}{12} ml^2$ 垂直于杆、通过杆端点的轴 $J=\dfrac 13 ml^2$
圆柱	$J=\dfrac 12 mR^2$
圆环	$J=mR^2$
球体 $^*$	$J=\dfrac 25 mR^2$
球壳 $^*$	$J=\dfrac 23 mR^2$

1.5. 刚体的定轴转动定律

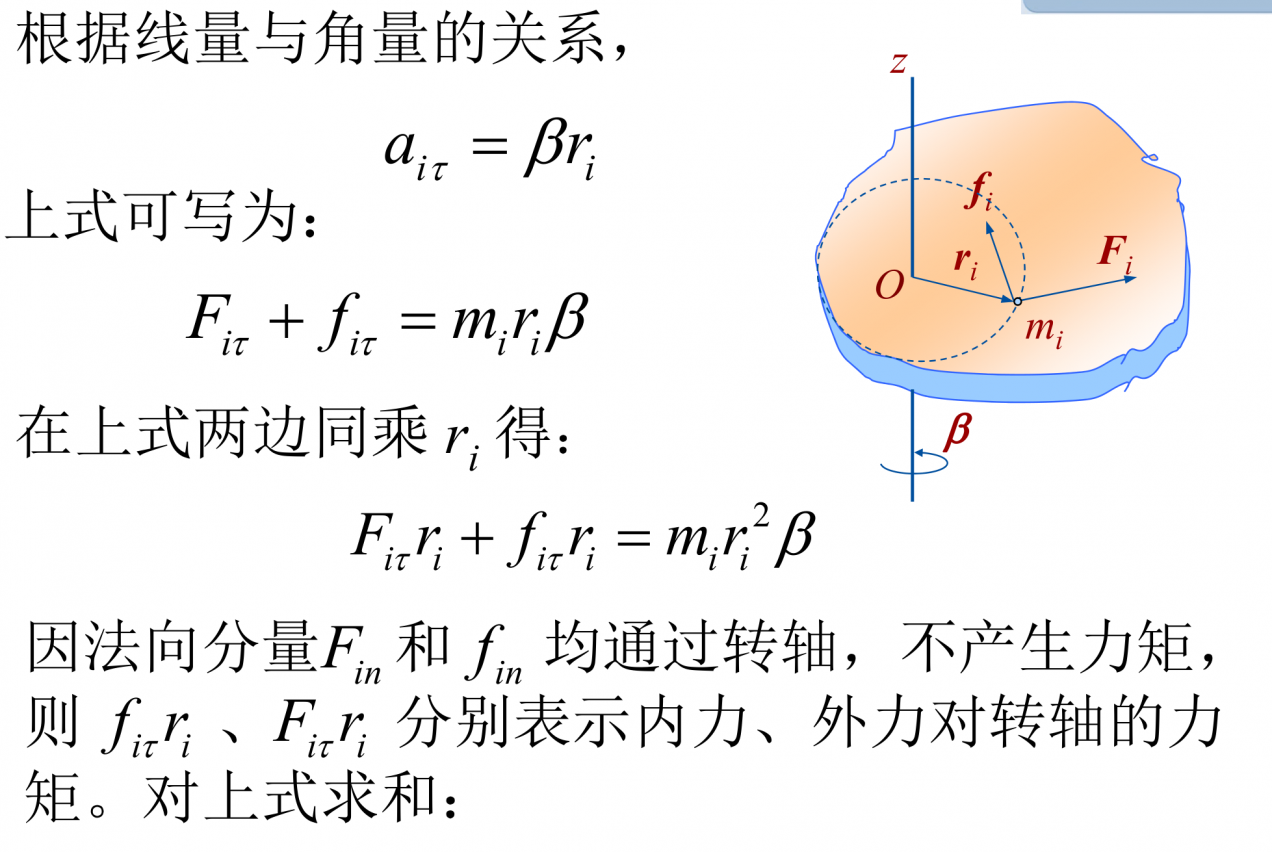
对轴的力矩： $\boldsymbol{M} = \boldsymbol{r} \times \boldsymbol{F}$ ，这里 $\boldsymbol{r}$ 垂直于定轴，力 $\boldsymbol{F}$ 在转动平面内，力矩 $\boldsymbol{M}$ 的方向沿着 $z$ 轴。

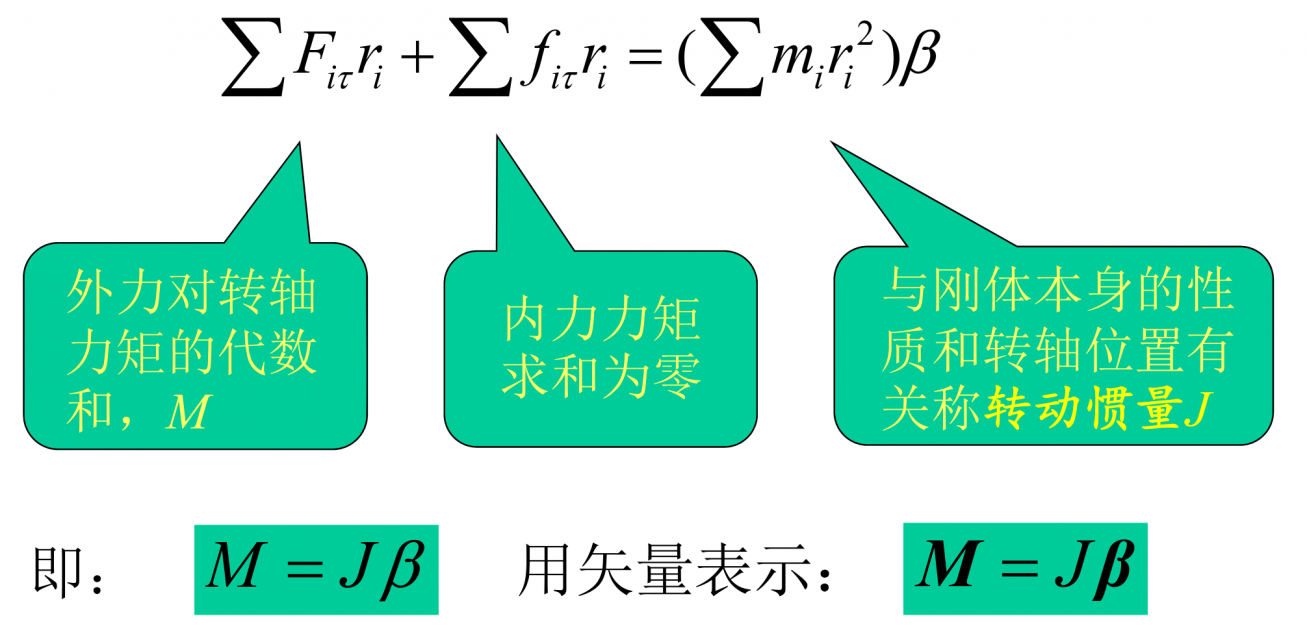
可以证明，内力的合力矩为零，故刚体所受的合力矩指外力的合力矩。 刚体的定轴转动定律： $\boldsymbol{M}_\text{外} = J \boldsymbol \beta$ 。

证明

1.6. 定轴转动的动能与动能定理

刚体定轴转动动能： $E_k=\dfrac{1}{2} J \omega^2$ 。

刚体定轴转动的动能可分解为绕通过质心轴的转动动能和随质心的平均动能。 $E_k=\dfrac{1}{2} J \omega^2 + \dfrac{1}{2} m v_C^2$ 。

刚体定轴转动的动能定理：合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。 $A=\dfrac{1}{2}J\omega^2 - \dfrac{1}{2}J\omega_0^2$ 。

1.7. 定轴转动的角动量定理和角动量守恒定理

刚体对轴的角动量：

\boldsymbol L = \sum m_i \boldsymbol v_i r_i = \sum m_i (\boldsymbol\omega r_i) r_i = \left(\sum m_i r_i^2\right)\boldsymbol\omega = J \boldsymbol \omega

定轴转动的角动量定理：

\boldsymbol M = \dfrac{\text d\boldsymbol L}{\text dt} = \dfrac{\text d(J\boldsymbol \omega)}{\text dt}

不要求转动惯量 $J$ 不变。
对角动量定理积分可得下面的角动量定理的积分形式。

定轴转动的角动量定理的积分形式：

\int_{t_0}^t \boldsymbol M \text dt =J \boldsymbol\omega - J_0 \boldsymbol\omega_0

$\int_{t_0}^t \boldsymbol M \text dt$ 为合外力矩对转轴的冲量矩。

定轴转动的角动量守恒定律：

\boldsymbol M = 0 \Rightarrow J \boldsymbol\omega = \text{常量}

1.8. 刚体的机械能守恒定律

当只有保守力的力矩作功时，刚体的总机械能守恒，即：

\frac{1}{2} J\omega^2 +mg h_c = \text{常量}\quad h_c \text{ 为刚体质心位置的高度}

1.9. 质点直线运动与刚体定轴转动的比较

质点直线运动	刚体定轴转动
速度 $\boldsymbol v=\dfrac{\text d\boldsymbol x}{\text dt}$	角速度 $\boldsymbol \omega = \dfrac{\text d\boldsymbol\varphi}{\text dt}$
加速度 $\boldsymbol a = \dfrac{\text d\boldsymbol v}{\text dt}$	角加速度 $\boldsymbol \beta = \dfrac{\text d\boldsymbol\omega}{\text dt}$
力 $\boldsymbol F$	力矩 $\boldsymbol M$
质量 $m$	转动惯量 $J$
牛顿第二定律 $\boldsymbol F = m \boldsymbol a$	转动定律 $\boldsymbol M = J \boldsymbol \beta$
动量 $\boldsymbol p=m\boldsymbol v$	角动量 $J\boldsymbol \omega$
冲量 $\boldsymbol I = \int_{t_0}^t \boldsymbol F \text dt$	冲量矩 $\int_{t_0}^t \boldsymbol M \text dt$
动量定理 $\int_{t_0}^t \boldsymbol F \text dt = m \boldsymbol v - m \boldsymbol v_0$	角动量定理 $\int_{t_0}^t \boldsymbol M \text dt = J \boldsymbol\omega - J \boldsymbol\omega_0$
平均动能 $\dfrac 12 m v^2$	转动动能 $\dfrac 12 J \omega^2$
力的功 $A=\int_{t_0}^t F \text dx$	力矩的功 $A=\int_{\theta_0}^\theta M \text d \theta$
动能定理 $A=\dfrac 12 m v^2 - \dfrac 12 m v_0^2$	动能定理 $A=\dfrac 12 J \omega^2 - \dfrac 12 J \omega_0^2$

1.10. 刚体的平面运动

刚体平面运动的动力学方程：可以分为质心的平动 $\boldsymbol{F}_\text{外} = m \boldsymbol{a_c}$ 和绕质心的转动 $\boldsymbol{M_{c\text{外}}} = J_c \boldsymbol{\beta}$ 。