本篇笔记主要介绍了质点力学的基本概念和运动学描述。首先定义了质点和参照系的概念,然后详细讲解了质点运动的描述方法,包括位置矢量、位移矢量、平均速度、瞬时速度和加速度等。接着重点讨论了圆周运动的描述,介绍了角速度、角加速度、切向加速度和法向加速度等概念。最后简要提到了自然坐标系下的加速度表示方法。这些基础知识为后续学习质点动力学奠定了基础。(由 claude-3.5-sonnet 生成摘要)
1. Ch2 质点运动学
解题指导
1.1. 质点与参照系
质点:具有质量而没有大小和形状的理想物体。
参照系:或称参考系。描述物体运动时选作参照的物体或系统。
- 为了定量确定物体的位置,还要在参照系上选取一个坐标系。
1.2. 质点运动的描述
位置矢量:简称位矢。用来确定物体位置。r=xi+yj+zk。
位移矢量:指终点位矢与起点位矢之差。Δr=r2−r1。
平均速度:v=ΔtΔr。
平均速率:v=ΔtΔs。
瞬时速度:质点位置矢量对时间的导数。v=dtdr。
瞬时加速度:质点速度矢量对时间导数。a=dtdv。
1.3. 圆周运动的描述
角速度:角坐标对时间的一阶导数。ω=dtdθ。单位 rad/s。
角加速度:角坐标对时间的二阶导数。β=dt2d2θ=dtdω。单位 rad/s2。
切向加速度:反应速度大小的变化。at=dtdv。
法向加速度:反应速度方向的变化。an=Rv2,这里 R 是曲率半径。(任意一无穷小段曲线,都可以看做一个圆上的一无穷小段圆弧,这个圆的半径称为曲率半径。)
- 在匀速圆周运动中,切向加速度为 0,向心加速度即法向加速度。
- 总加速度 a 的大小为:a=an2+at2。
- a 与 v 的夹角为:tanθ=atan。
1.4. 自然坐标系下的加速度表示
自然坐标系:在轨道上任取一点做原点 O,在 t 时刻质点位置可用 P 点到 O 点的曲线长度 s 表示。
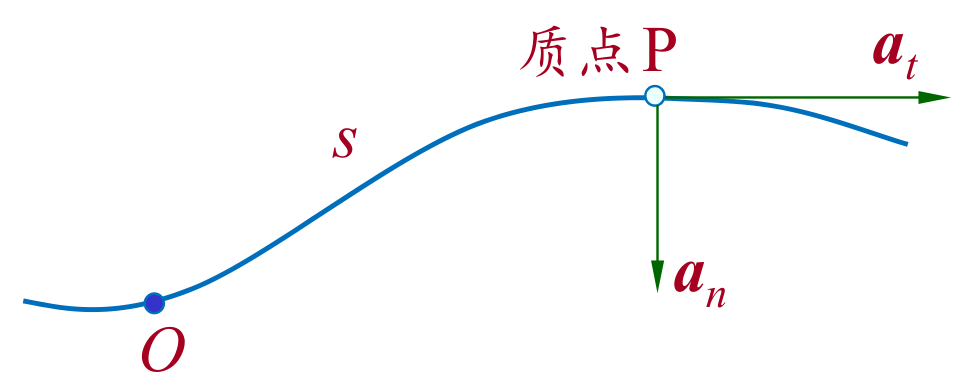
曲率半径:ρ=dθds。
由变速圆周运动的结果可得一般曲线运动的加速度:
a=atτ+ann=dtdvτ+ρv2n
2. Ch3 动量·动量守恒定律
解题指导
2.1. 牛顿第一定律(惯性定律)
牛顿第一定律(惯性定律):任何物体,只要没有外力改变它的状态,便将永远保持静止或匀速直线运动状态。
惯性参照系:简称惯性系。惯性定律成立的参考系。
- 一切相对于惯性系作匀速直线运动的参考系都是惯性系。
2.2. 牛顿第二定律
动量:p=mv。
牛顿第二定律:在合力 F 的作用下,质点动量随时间的变化率等于作用于之间的合力。
F=dtdp=mdtdv
- 牛顿第二定律只适用于惯性系。
- 经典物理中 m 为常量,故第二个等号在高速运动的情况下不适用。
2.3. 牛顿第三定律
牛顿第三定律:作用力与反作用力大小相等,方向相反,且作用在同一直线上。即 F12=−F21。
2.4. 力的相对性原理
力的相对性原理:在惯性系中进行力学实验,无法确定惯性系之间的相对速度。或,力学定律在惯性系中具有相同的形式。或,力学定律对惯性系变换具有不变性。或,所有的惯性系都是等价的。
2.5. 非惯性系中的力学定律
在加速平动非惯性系中,我们牛顿定律不成立,我们可以引进一假想的惯性力,使非惯性系中的牛顿定律成立:
FI=−maI
- 惯性力的大小为质量 m 与牵连加速度大小 aI 的乘积,方向与 aI 相反。
- 惯性力没有施力者,也没有反作用力。
2.6. 动量定律
动量:p=mv。
讨论力的时间积累效果,将牛顿第二定律改写成 Fdt=dp,在 t0∼t 的时间段内积分,得:
∫t0tFdt=p−p0=mv−mv0
冲量:力对时间的积分,描述一段时间内力对时间的累积作用。I=∫t0tFdt。
质点动量定律:一段时间内质点所受合力的冲量等于这段时间内质点动量的增量。即 I=p−p0=Δp。
冲力:在碰撞、打击等过程中的相互作用力称为冲力,由于冲力的作用时间短,我们引入平均冲力的概念:
F=t−t0I
2.7. 动量守恒定律
动量守恒定律:合外力为零时,质点系的总动量保持不变。
F=0时,p=i∑mvi=常矢量
在某一方向上外力为零时,则动量守恒定律在这一方向上成立。
2.8. 质心与质心运动定律
质心:质点系的质量中心。质心的位置是质点系内各质点的质量的带权平均值,即:
rc=∑mi∑miri=m∑miri
质心运动定律:质点系所受的合外力等于质点系总质量与质心加速度的乘积。
- 动量守恒定律另一种表达形式:质点系所受的合外力为零,则质心速度保持不变。
2.9. 质心参照系
质心参照系:原点选在质心上的平动参照系,称为质心参照系(与惯性系只有相对平动)。
- 在质心参照系中质心速度恒定为零:vc′=0。
- 质心参照系中总动量恒定为零:p=mvc′=0。
2.10. 米舍尔斯基方程与火箭运动
米舍尔斯基方程:研究主体质量及其流动问题:设 t 时刻主体质量 m、速度为 u,dt 时间内有质量为 dm,速度为 dv 的流动物加到主体上。在 (t+dt) 时刻,主体质量变为 (m+dm),速度为 (u+du)。设主体受外力 F,则有
mdtdu=F+(v−u)dtdm
- 其中,v′=v−u 表示流动物即将加到主体上时相对于主体的速度,dtdu 为主体加速度,dtdm 为主体质量随时间的变化率。
- 以 dm 为研究对象,在 dt 的时间内有 dtdp=−v′dtdm。这个反作用力 v′dtdm 就是 dm 对主体的作用力。
证明
3. Ch4 能量·能量守恒定律
解题指导
3.1. 功与功率
功:功是力的空间积累。
A=F⋅Δr=F∣Δr∣cosθ
- 功是过程量,与路径有关。合力的功为各分力功的代数和。
功率:单位时间内做的功。
P=dtdA=F⋅dtdr=F⋅v
3.2. 动能与动量定理
动能:关于运动状态的函数。质点动能 Ek=21mv2。
质点动能定理:合外力对质点做的功等于质点动能的增量。
WAB=EkB−EkA
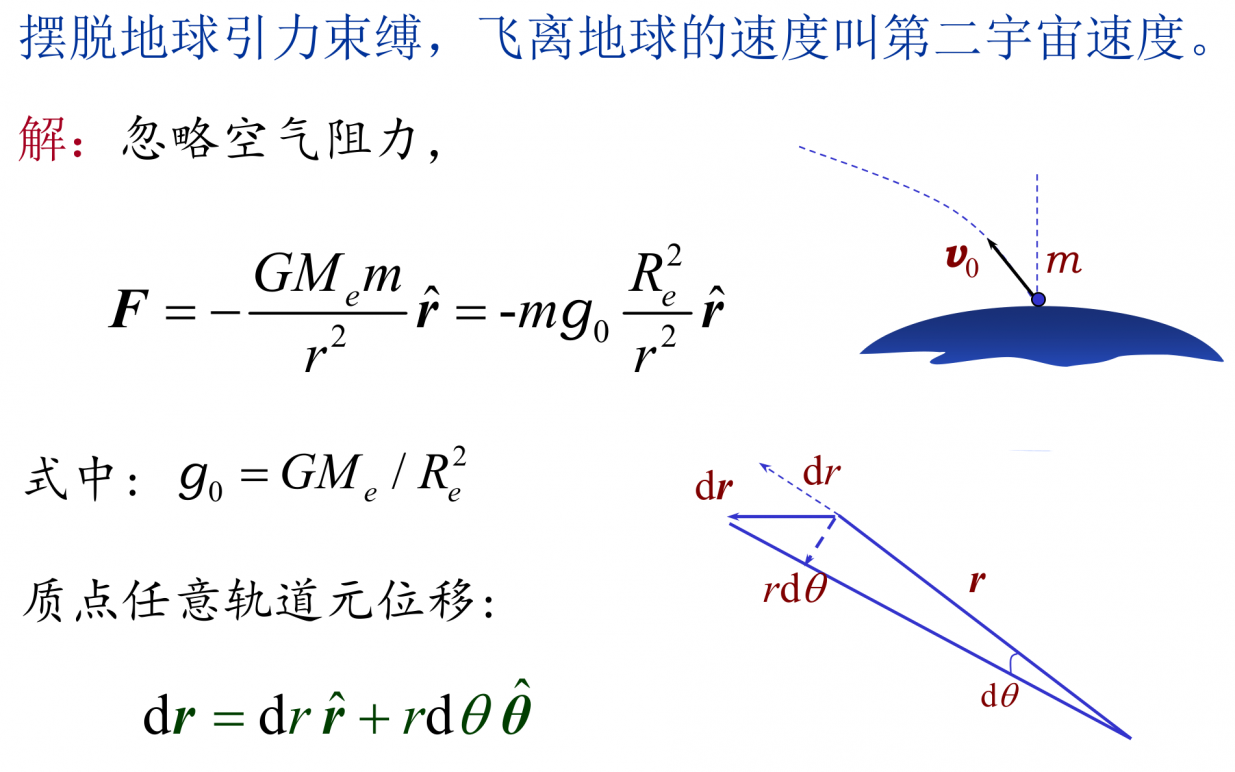
逃逸速度问题(第二宇宙速度)
3.3. 保守力
保守力:凡成对作用力和反作用力的做功之和与路径无关,只决定于始末相对位置的力称为保守力;或者说,保守力沿着任意闭合回路的做功为零。
- 保守力所作的功可以通过势能的变化来量度。
- 给出保守力的一些充分条件:
-
- 对于一维运动,凡是位置 x 的单值函数的力都是保守力,如弹性力。
-
- 对于一维以上的运动,大小和方向都与位置无关的力都是保守力,如重力 G=mg。
-
- 凡是“有心力”都是保守力。
3.4. 势能与一维势能公式
势能:由于成对保守力做功只决定于始末态的位置,可引进一个关于位置的状态函数:势能 Ep。定义:在系统相对位置变化的过程中,成对保守内力做功之和等于系统势能增量的负值。
- 只有内力是保守力,才能引入势能。
- 势能在大小上只有相对意义,所以势能零点的选择是任意的。
系统的势能:系统在任意位置的势能等于从该位置沿任意路径变到势能零点的过程中保守内力所做的功。
力学中的几种势能:引力势能:Ep=−Grm1m2;重力势能:Ep=mgh;弹性势能:Ep=21kx2。
一维势能公式:Ep(x)=∫xx0F(x)dx,其中 x 为任意点 P 的位置,x0 为参考点的位置。求导得到:F(x)=−dxdEp(x)。
- 物体只能在势能低于总机械能的范围内运动。
- 势能曲线的极小值对应于稳定平衡点,极大值对应于不稳定平衡点。
3.5. 机械能守恒定律
质点系的动能定理:外力作功和内力作功之和等于质点系动能的增量。
A外+A内=Ek−Ek0
功能原理:外力作功和非保守内力作功之和等于系统机械能的增量。
A外+A内非=(Ek+Ep)−(Ek0−Ep0)
机械能守恒定律:如果只有保守内力作功,而外力和非保守内力不做工,那么系统的动能和势能可以相互转化,但总机械能保持不变。
A外+A内非=0⇒Ek+Ep=Ek0+Ep0=常量
4. Ch5 角动量·角动量守恒定律
解题指导
4.1. 角动量
质点的角动量:质点对惯性系中任一固定点的角动量 L 定义为位矢 r 与动量 p 的叉积。
L=r×p=r×mv
- 其大小可以表示为 L=rmvsinθ,其中 θ 为速度与法线的夹角。
- 角动量 L 的方向满足右手螺旋定则。
4.2. 力矩
力矩:力矩 M 表征力 F 使物体绕参考点 O(相对于该点取矩)转动的能力。M=r×F。
4.3. 角动量定理
角动量定理:质点角动量对时间的变化率等于质点所受的合力矩。
M=dtdL
4.4. 角动量守恒定律
角动量守恒定律:对某一固定点,若质点所受合力矩为零,则质点对该固定点的角动量守恒。
M=0⇒L=常矢量
5. Ch7 万有引力
解题指导
5.1. 万有引力定律
引力常数:G=6.67×10−11N⋅m2/kg2。
万有引力定律:设 r^ 为位矢方向的单位矢量,负号表示万有引力的方向与 r^ 的方向始终相反。
F=−Gr2Mm
5.2. 引力势能
选无穷远处为零势能点,有
U=−GrMm
5.3. 开普勒行星运动定律
开普勒第一定律(轨道定律):行星沿着椭圆轨道运行,恒星位于椭圆的一个焦点上。
开普勒第二定律(面积定律):任何行星到太阳的矢径在相等的时间内扫过相等的面积(掠面速度不变)。
开普勒第三定律:椭圆轨道半长轴 a 的立方与周期 T 的平方成正比,其比值是与行星性质无关的常量,即 T2a3=K。
5.4. 惯性质量与引力质量
m惯=m引
惯性力与引力等效。