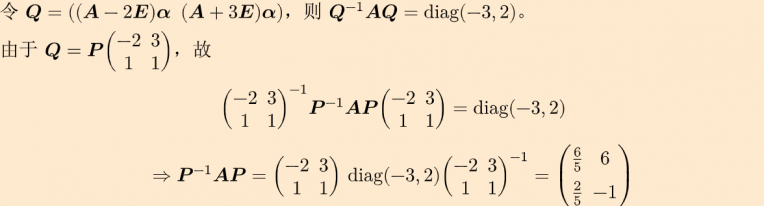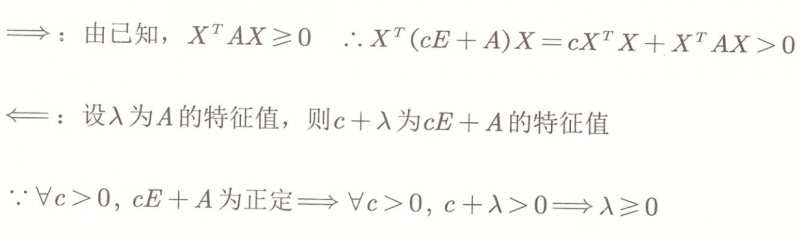1. 秩为 1 的矩阵的相似对角化

设 $\alpha = [1,2,3,4]^T,\,\beta = [3,-2,-1,a]^T,\,A=\alpha\beta^T$，问当 $a=(\quad)$ 时 $A$ 能对角化？

2. 相似对角化相关计算

【2012-2013 春夏期末】设 $A_{3\times 3}$ 满足 $A \alpha_1=0,\,A \alpha_2 = 2 \alpha_1+\alpha_2,\,A \alpha_3 = -\alpha_1 + 3 \alpha_2 - \alpha_3$。其中 $\alpha_1=[1,1,0]^T,\,\alpha_2=[0,1,1]^T,\,\alpha_3=[1,1,1]^T$。问：

1. $A$ 能否对角化；
2. 求 $A$。

3. 矩阵论与线性空间结合证明

证明：$A_{n\times n}^2 = E \,\Leftrightarrow\, r(A+E) + r(A-E)=n$，再求 $|A+5E|$。

4. 正定矩阵的性质

【2020-2021 秋冬 8】设 $A,B$ 都是实对称矩阵且 $A$ 正定，试证明 $AB$ 可相似对角化。

5. 用相似对角化作突破口

【P129 习题五 31】设 $A \in \mathbb P^{2 \times 2},\ P = (\alpha \quad A\alpha)$，其中 $\alpha$ 是非零向量且不是 $A$ 的特征向量。已知 $A^2 \alpha +A \alpha - 6 \alpha = \theta$，求 $P^{-1} A P$。

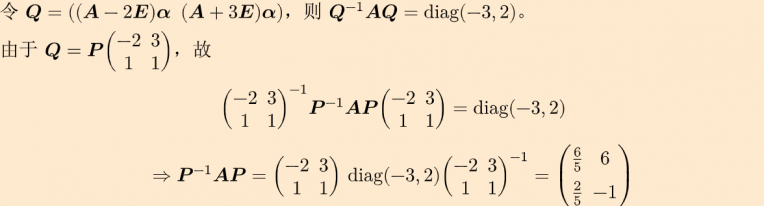
6. 反对称实矩阵的特征值

【P133 习题五 58】证明：反对称实矩阵的特征值或为零，或为虚部不为零的纯虚数。

7. 特征值性质的简单应用

1. 填空：设二阶矩阵 $A$ 的特征值是 $\lambda_1=1,\lambda_2=2$，则行列式 $|A^2-3A+4E|$ 的值为（$\quad$）。
2. 判断：若方阵 $A$ 满足 $A^2+4A+4E=O$，则 $A$ 的特征值仅为 $-2$。（$\quad$）

8. 正定矩阵的判定

证明：设 $A$ 是 $n\times m$ 阶实矩阵，证明 $A^T A$ 半正定。

9. 正定二次型的判定

设 $f(x_1,x_2,\dots,x_n) = (x_1+a_1x_2)^2 + (x_2+a_2x_3)^2 + \cdots + (x_n+a_nx_1)^2$ 是实二次型，其中 $a_1,a_2,\dots,a_n$ 为实数，则下面选项正确的是（$\quad$）。

A. 当 $a_i\neq 0\,(i=1,2,\dots,n)$ 时 $f(x_1,x_2,\dots,x_n)$ 为正定二次型。
B. 当 $a_1 a_2 \cdots a_n \neq (-1)^n$ 时 $f(x_1,x_2,\dots,x_n)$ 为正定二次型。
C. 当 $a_i>0\,(i=1,2,\dots,n)$ 时 $f(x_1,x_2,\dots,x_n)$ 为正定二次型。
D. 当 $a_i<0\, (i=1,2,\dots,n)$ 时 $f(x_1,x_2,\dots,x_n)$ 为正定二次型。

10. 特征值都是实数

【2021-2022 秋冬期末】 (1) $A$ 是 $n$ 阶实对称矩阵，$B$ 是 $n$ 阶正定矩阵，证明：矩阵 $AB$ 的特征值均为实数。

11. 正定矩阵的定义

【2017-2018 秋冬期末】 设 $A$ 为 $n$ 阶实对称矩阵，试证明 $A$ 半正定当且仅当 $\forall c > 0$，$cE+A$ 正定。

12. 相似对角化相关压轴题

都有一定难度和思考价值，这里就不一一截取证明过程了，可以自行参考历年卷答案。

【2020-2021 秋冬期末】 设 $A,B$ 都是 $n$ 阶实对称矩阵且 $A$ 正定，试证明 $AB$ 可相似对角化。

【2019-2020 秋冬期末】设 $A$ 是一个 $n$ 阶方阵（$n\ge 2$），$A^*$ 是 $A$ 的伴随矩阵且满足 $A_{11} \neq 0$，是一个 $n$ 维非零列向量，试证明：非齐次线性方程组 $AX=\alpha$ 有无穷多解当且仅当 $\alpha$ 是齐次方程组 $A^* X=0$ 的解。

【2019-2020 春夏期末】 设 $A$ 是一个 $n$ 阶实矩阵，试证明 $A$ 是反对称矩阵当且仅当 $AA^T=-A^2$。

【2019-2020 春夏期末】 设 $C$ 是 $n$ 阶正定矩阵，$B$ 是满足 $BB^T=-B^2$ 的 $n$ 阶实矩阵，试证明 $C+B$ 可逆。