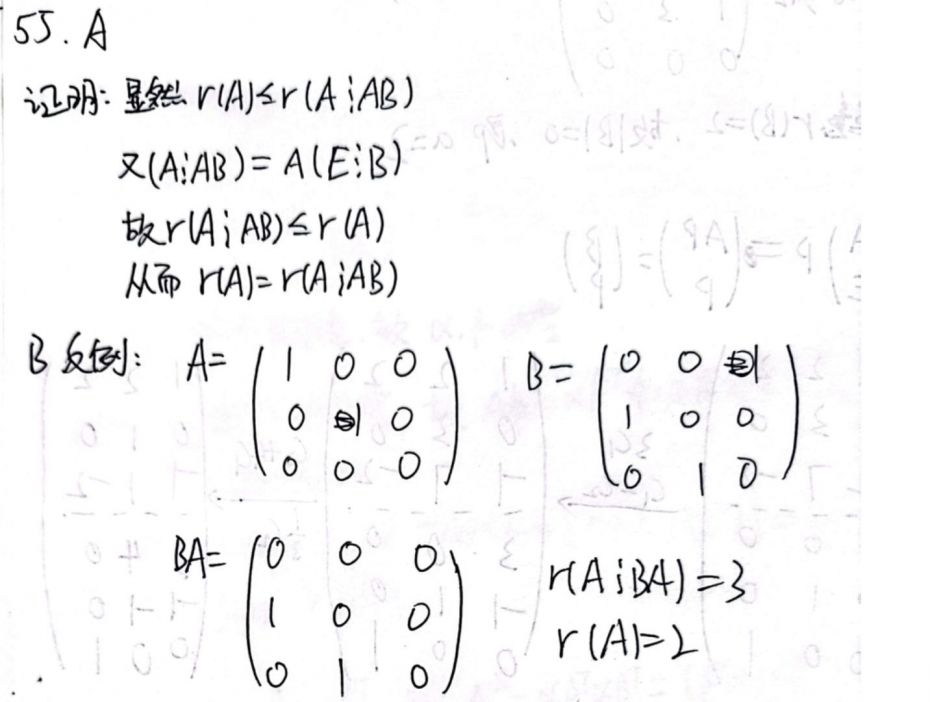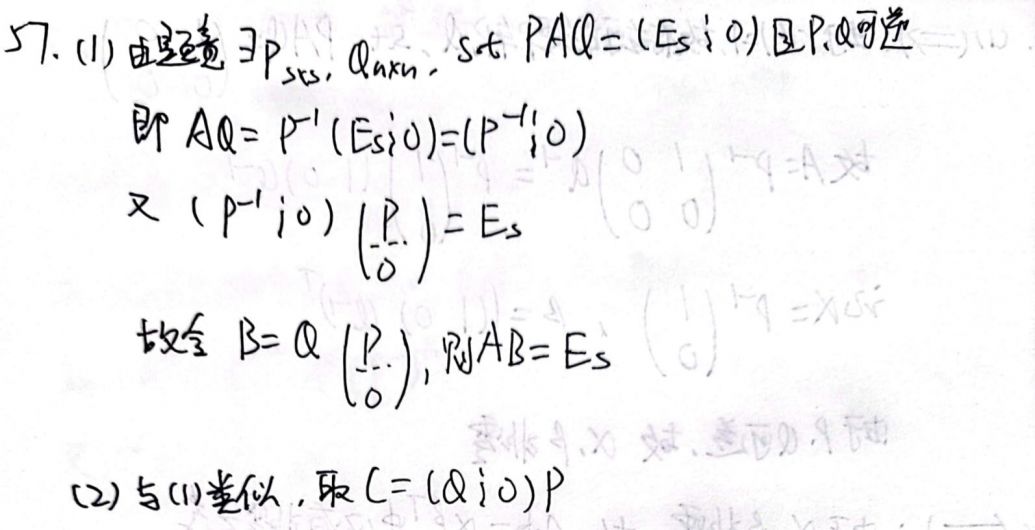I 线性方程组、矩阵的秩和行列式

1. 关于伴随矩阵的秩的重要结论

【P74 习题三 60】设 $A$ 为 $n$ 阶矩阵（ $n\ge 2$ ）， $A^*$ 为 $A$ 的伴随矩阵，证明：

r(A^*) = \left\{ \begin{aligned} &n,&&r(A)=n\\ &1,&&r(A)=n-1\\ &0,&&r(A)\le n-2\\ \end{aligned} \right.

想不到吧？

可以利用相抵标准形证明。

答案

【P73 习题三 55】设 $A,B$ 为 $n$ 阶矩阵，则（ $\quad$ ）

A. $r(A\,\, AB)=r(A)$ 。
B. $r(A\,\, BA)=r(A)$ 。
C. $r(A\,\, B) = \max\{r(A),r(B)\}$ 。
D. $r(A\,\,B)=r(A^T\,\,B^T)$ 。

注意

这题中 (A) 选项是正确的而 (B) 选项是错误的。看似 (A) 选项的证明过程迁移过来也可以证明 (B) 选项正确，但实际上中间某步矩阵乘法会不满足左矩阵的行数等于右矩阵的列数。

答案

【P75 补充题三 11】设矩阵 $A\in \mathbb P^{m\times n},\, B \in \mathbb P^{n\times m}$ ，试证明：

r(E_m - AB) + n = r(E_n-BA) + m

思路

写出分块矩阵 $\begin{bmatrix}E_n & B\\ A & E_m\end{bmatrix}$ ，对其应用初等变换不改变秩，将其化为想要的形式即可。这充分利用了 $A$ 是 $m\times n$ 矩阵而 $B$ 是 $n\times m$ 矩阵的条件。

答案

【P73 习题三 57】设 $A$ 是一个 $s\times n$ 矩阵，证明：

如果 $s\le n$ 且 $r(A)=s$ （此时称矩阵 $A$ 是行满秩的），那么必有 $n\times s$ 矩阵 $B$ 使得 $AB=E_s$ 。
如果 $n\le s$ 且 $r(A)=n$ （此时称矩阵 $A$ 是列满秩的），那么必有 $n\times s$ 矩阵 $C$ 使得 $CA = E_n$ 。

两点提醒

答案

【P75 补充题三 11】试证明 $\mathbb P^{n\times n}$ 中任意一个矩阵均可表示为 $\mathbb P^{n \times n}$ 中的一个可逆矩阵和一个幂等矩阵的乘积。

幂等矩阵的充要条件

$A$ 是幂等矩阵的充要条件是存在可逆矩阵 $T$ 使得 $T^{-1} \begin{bmatrix}E_r&\\ &O_{n-r}\end{bmatrix} T$ ，即 $A$ 与 $\begin{bmatrix}E_r&\\ &O_{n-r}\end{bmatrix}$ 相似。

答案

【P75 补充题三 5】设分块矩阵 $\begin{bmatrix}A & B\\ C & D\end{bmatrix}$ 是对称矩阵，且 $A$ 可逆，证明：存在可逆矩阵 $P$ 使得

P^T \begin{bmatrix}A&B\\ C&D\end{bmatrix}P =\begin{bmatrix}A&O\\O&D-CA^{-1}B\end{bmatrix}

答案