本篇笔记概括了「数据结构基础」课程中的重要概念，包括算法分析、线性结构、树、堆、排序、哈希、并查集和图等内容。每个章节详细介绍了相关的定义、特性和操作，帮助读者理解和掌握数据结构的基本知识和应用。（由 gpt-4o-mini 生成摘要）

Ch02 Algorithm Analysis

算法(algorithm)：完成特定任务的有限步指令。所有的算法都具备以下特征：

• 输入(input)：0 个或多个输入
• 输出(output)：至少有 1 个输出
• 确定性(definiteness)：每条指令都是明确的
• 有限性(finiteness)：不管什么在什么情况下，算法需要在经过有限步后终止
• 有效性(effectiveness)：每条指令足够简单可行，原则上使用纸和笔便能表达出来。

Ch03 Linear Structures

Queue

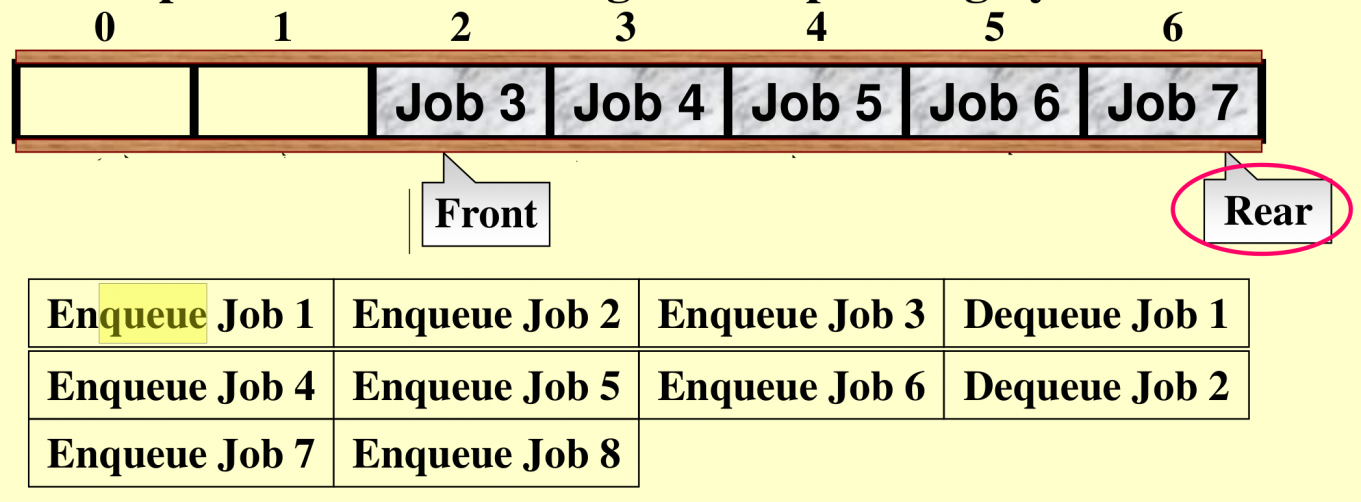
初始状态 front == 0，rear == -1。

Circular Queue

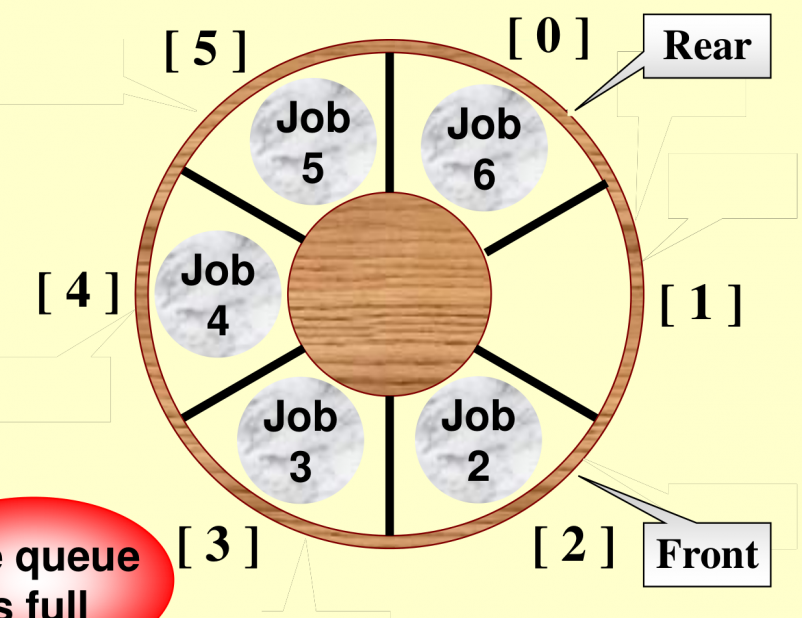
这种实现要求至少留一个空位置。

• 初始状态：front = 1，rear == 0（需要相差 1）
• 判断空：(rear + 1) % size == front
• 判断满：(rear + 2) % size == front
• 如果额外记录一个 size 来判断空和满，就可以不用留一个空位置。

Ch04 Trees

Trees

• 顶点 $x$ 的深度(depth)：从根节点出发到 $x$ ​ 的路径长度，规定 $\text{depth}(root)=0$。

• 顶点 $x$ ​ 的高度(height)：从 $x$ ​ 到叶子结点的最长路径长度，规定 $\text{height}(leaf)=0$。

• 祖先(ancestor)：从该节点到根节点的路径上所有的节点

• 后代(descendant)：该节点所有子树的节点

树的表示：

• List Representation：一般的链表
• FirstChild-NextSibling Representation：左孩子右兄弟
  • 可以用来把普通的树转为二叉树表示。

Binary Trees

• full：每个节点要么没有孩子要么有两个孩子。
• complete：所有叶子节点的深度差一，且尽可能在左边（$n$ 个点的 complete binary tree 就是 perfect binary tree 的前 $n$ 个节点）。
• perfect：所有叶子节点深度相同。

Threaded Binary Trees：在记录二叉树的时候，如果左孩子指针是空的，就将其指向中序遍历里的前一个；如果右孩子指针是空的，就将其指向中序遍历里的后一个。如果中序遍历里没有前驱后继，就连向根节点。

二叉搜索树的删除操作：

• 删除叶子节点：直接让他的父亲节点连到空节点上。
• 删除只有一个孩子的节点：用该节点的子节点替换它自身。
• 删除有两个孩子的节点：用该节点的左子树最大节点或右子树最小节点替换自身，用来替换的节点用上面两条方法删除。

Ch05 Heaps

以小根堆为例：

• Percolate Up：只要当前节点的值比其父亲节点小，就进行交换，如此递归。
• Percolate Down：只要当前节点的值比其较小孩子节点大，就进行交换，如此递归。
• 线性建堆：从最后一个有孩子的节点开始往前，依次执行 percolate down 操作。

Ch06 Sorting

Insertion Sort

插入排序是 $O(I+n)$ 的，这里 $I$ 是逆序对个数。

Shellsort

$k$-sort 指的是间距为 $k$ 的一轮插入排序。

希尔排序的最坏复杂度是 $\Theta(n^2)$ 的。但如果我们选用 Hibbard’s Increment Sequence（$h_k=2^k-1$），可以证明最坏复杂度是 $\Theta(n^{3/2})$ 的。

Heap Sort

对于随机数据，平均比较次数是 $2n\log n-O(n\log \log n)$ 的。

Quick Sort

pivot 的选取策略：

• 随机选取：但是生成随机数的代价比较高。
• Median-of-Three Partitioning：从左边、中间、右边的三个数中选一个中位数来当 pivot。

需要注意的细节：

• A[Left]、A[Center]、A[Right] 在这里就已经排序。
• 把 pivot 放在 A[Right - 1] 的位置。
• 只需要对 A[Left + 1] 到 A[Right - 2] 的部分进行排序。

Radix Sort

Least Significant Digit：低位到高位排序。每次桶排完按顺序合并成一条队列，然后继续 radix sort。 Most Significant Digit：高位到低位排序。每次桶排完对每个桶分别继续应用排序算法。

Ch07 Hashing

• 标识符密度(identifier density)：$\dfrac{n}{T}$。

• 加载密度(loading density)：$\lambda=\dfrac{n}{s\cdot b}$。当 $\lambda =1$ 时哈希表满，再插入数会发生 overflow。

• 冲突(collision)：想放入的某数和已经有的某数有相同的哈希值（即 $f(i_1)=f(i_2)$ 且 $i_1\neq i_2$）。

• 溢出(overflow)：某一个数已经无法加入哈希表中。

单独链表法(separate chaining)：将所有散列值相同的键放入同一张链表中。

开放地址法(open addressing)：寻找下一空的单元存放，枚举 $i$ 直到位置 $\text{hash}(x)+f(i)\bmod TableSize$ 可放（注意都是对 table size 取模）。

• linear probing：$f(i)=i$
  • 导致 primary clustering：形成较大的 cluster，从而大大降低插入和查询的性能。
• quadratic problem：$f(i)=i^2$
  • 可以证明：如果 $TableSize$ 是质数，那么在插入不超过 $\lfloor TableSize/2\rfloor$ 个数的情况，一定能找到位置放。
  • 可以证明：如果 $TableSize$ 是形如 $4k+3$ 的质数，那么哈希表在没满之前，都一定能找到位置放。
• double hashing：和正常理解的双哈希不太一样，这里是指 probing 函数是 $f(i)=i\times \text{hash}_2(x)$。
  • 可以使用 $\text{hash}_2(x)=R-(x\%R)$，这里 $R$ 是一个比 $TableSize$ 小的质数。
• 如果需要支持删除操作，只能通过打懒标记的方式。

Rehashing

何时使用 rehashing？

• 被占用的表空间达到一半时
• 插入失败时
• 散列表的加载因数 $\lambda$ 达到特定值时

rehashing 的过程：

• 建立一张额外的表，大小是大于原大小两倍的第一个质数。
• 遍历原来的整张散列表中未删除的元素
• 使用新的散列函数，将遍历到的元素插入新的表中

Ch08 Disjoint Sets

合并策略：

• union-by-size：记录 S[root] = -size，合并的时候比较两个根节点的 size，把小的合并到大的上。
  • $n$ 次 union 操作和 $m$ 次 find 操作的总时间复杂度为 $O(n+m\log n)$（这里 union 操作里的 find 也算在 $m$ 里）。
• union-by-height：记录树高然后根据树高合并。
• union-by-rank：其实就是 union-by-height，但是由于路径压缩的缘故，可能已经不是真实的 height。
• 如果比较时两边用于比较的参数相等，那么让第二个参数所在的并查集挂到第一个参数所在的并查集上。
• 进行 merge 操作的时候注意检查两个点是否已经在同一个等价类内。

路径压缩(path compression)：在 find 的时候会吧路径上的点都挂到根上。

对于同时应用了 union-by-rank 和 path compression 的并查集，其 find 操作的时间复杂度是 $\alpha(n)$ 的。

Ch09 Graphs

Graph Terminologies

表示图的方法：

• Adjacency Matrix

• Adjacency Lists

• Adjacency Multilists

• 稀疏(sparse)

• 稠密(dense)

Shortest Path

Dijkstra 算法的不同实现与复杂度：

• 朴素做法：$O(|V|^2+|E|)$
• 使用堆维护，每次更新距离时用 decrese key 的方式：$O(|V|\log |V|+|E|\log|V|)=O(|E|\log |V|)$。
• 使用优先队列维护，每次 delete min 直到出现一个没有更新过的点：$O(|E|\log |E|)$。

Network Flow

原图、流量网络、残量网络：

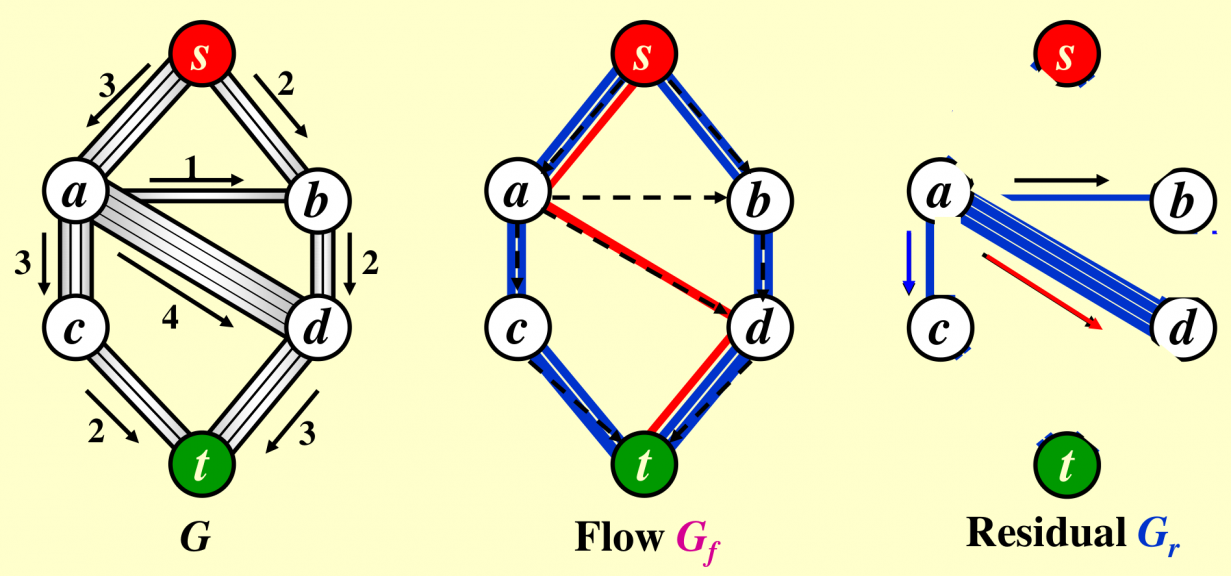
Biconnected Components

• 关节点(articulation point)：割点
• 双联通分量(biconnected component)：（点）双联通分量，可能有一个点在多个双联通分量内。每个双联通分量是一个极大的不存在割点的联通子图。

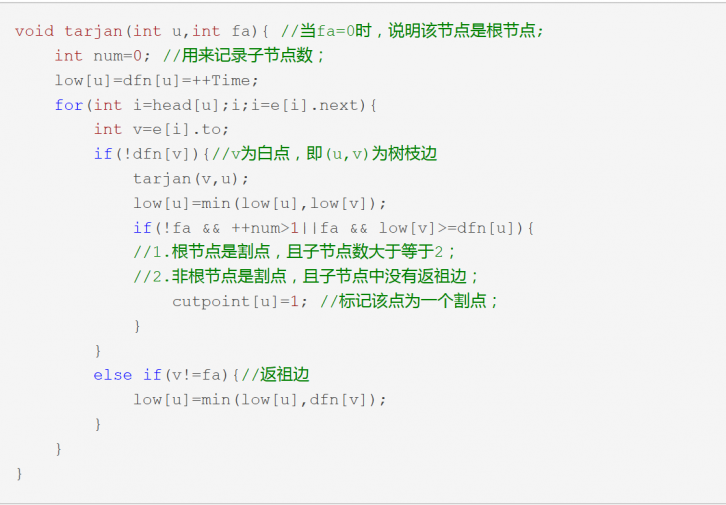
用 Tarjan 算法找点双的方法：

• $Num(u)$ 记录访问到这个点的时间戳。
• $Low(u) = \min\{Num(u),\min\{Low(v)|v\text{ 是孩子}\}, \min\{Num(v)|(u,v)\text{ 是返祖边}\}\}$。
• 一个点是割点当且仅当：
  • 该点是根节点且子节点数量大于等于 $2$。
  • 该点是非根节点且存在子树满足子树内没有到当前节点祖先的返祖边（即 $Low(v)\ge Num(u)$）。