本篇笔记介绍了集合的基本概念,包括集合的定义、表示方法、集合之间的关系、集合的操作以及函数的基本性质。我们探讨了集合的基数、可数性以及康托定理等重要主题。通过这些内容,读者将能够理解离散数学中集合和函数的基本结构和性质。(由 gpt-4o-mini 生成摘要)
Word Table
1. 集合 Sets
1.1. 引言 Introduction
集合(set):A set is an unordered collection of objects.
- The objects in a set are call the 元素(elements),or members, of the set.
- A set is said to 包含(contain) its elements.
- : is the member of the set .
- : is not the member of the set .
- 空集(empty set):.
集合的表示方式:The descriptions of a set
- Roster method: listing all its members between braces, e.g. .
- Brace notation with ellipses: e.g. .
- Specification using set builder: , which means contains all the elements from (全集(universal set)) which have the property .
- 维恩图(Venn diagrams)
Suppose there is a town with just one male barber; and that every man in the town keeps himself clean-shaven: some by shaving themselves, some by attending the barber. The barber obeys the following rule: he shaves all and only those men in town who do not shave themselves. Does the barber shave himself? 罗素悖论 Russell Paradox
1.2. 集合之间的关系 Relations between Sets
1.2.1. Subset
: is a 子集(subset) of the set .
1.2.2. Equal
: is 等于(equal) to .
1.2.3. Proper Subset
: A is a 真子集(proper subset) of the set .
1.2.4. The Size of Sets
Let be a set. If there are exactly distinct elements in where is a nonnegative integer, we say that is a 有限集(finite set) and that is the cardinality of .
1.2.5. Power Sets
Given a set S, the 幂集(power set) of S is the set of all subsets of the set S. denotes the power set of .
证明:.
1.2.6. Cartesian Products
The 有序 元组(ordered -tuple) is the ordered collection that has as its first element, as its second element, … , and as its nth element.
的笛卡尔积(cartesian product) 定义为
- If , then .
1.2.7. Truth Sets of Quantifiers
Given a predicate and a domain . The 真集(truth set) of is is the set of elements in for which is true. Namely, the power set of is
1.3. 集合操作 Set Operations
1.3.1. Union
1.3.2. Intersection
1.3.3. Difference
: The difference of and .
1.3.4. Complement
: is the 补集(complement) of the set .
1.3.5. Symmetric difference
按出现与否统计的话就类似于异或操作。
1.4. 集合恒等式 Set Indentities
更多集合恒等式(set indentities) 可以参考逻辑恒等式。
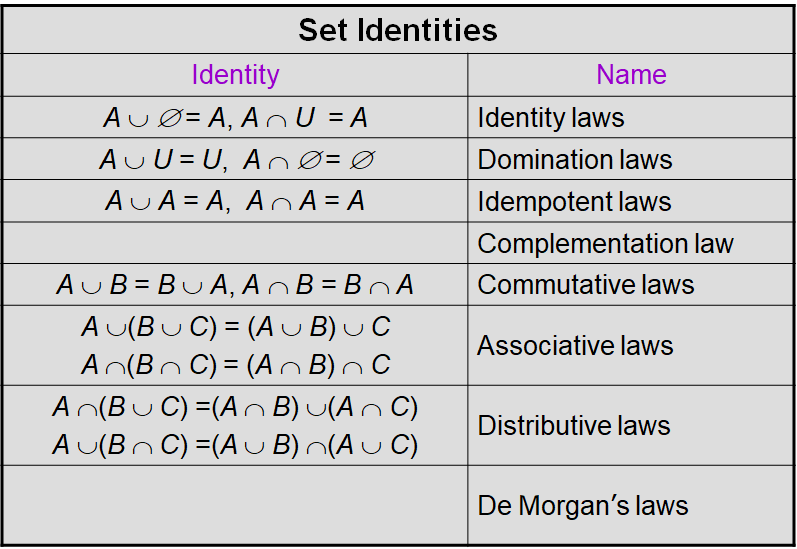
证明集合相等的一些方法 Ways to Prove Set Identities
2. 函数 Functions
2.1. 引言 Introduction
Let and be nonempty sets. A 函数(function) (mapping or transformations) from to :
- is called the 定义域(domain) of
- is called the 值域(codomain) of
If ,
- is called the image of under .
- is called a preimage of .
Let be a function from the set to the set . The 图(graph) of the function is the set of ordered pairs
2.2. 单射与满射 One-to-One and Onto Functions
A function f is 单射函数(one-to-one function = injection) (denoted 1-1), or 单射的(injective) if
A function from to is called 满射函数(onto function = surjection), or 满射的(surjective) if
The function f is a 一一对应的(one-to-one correspondence), or a 双射(bijection), if it is both one-to-one and onto.
Showing that is one-to-one or onto

2.3. 反函数 Inverse Functions
Let be a bijection from to . Then the 反函数(inverse function) of , denoted as , is the function from to defined as
- 函数 的反函数存在当且仅当函数 是双射函数。Function is 可逆的(invertible) if and only if is bijective. No inverse function exists unless is a bijection.
2.4. 函数的复合 Compositions of Functions
Let be a function from the set to the set and let be a function form the set to the set . The composition of the functions and denoted by is defined by:
- can’t be defined unless the range of is a subset of the domain of .
2.5. 高斯函数 Floor and Ceiling Functions
关于高斯函数的实用性质 Useful Properties of the Floor and Ceiling Functions

3. 数列 Sequence
3.1. 引言 Introduction
A 数列(sequence) is a function from a subset of the set of integers (usually either the set or the set ) to a set . We use the notation to denote the image of the integer . We call an a term of the sequence.
A 等比数列(geometric progression) is a sequence of the form
where the initial term and the 公比(common ratio) are real numbers.
An 等差数列(arithmetic progression) is a sequence of the form
where the initial term and the 公差(common difference) are real numbers.
3.2. 和式 Summations
: the subset of the domain of the function
Some Useful Summation Formulae

4. 集合的基数 Cardinality of Sets
4.1. 引言 Introduction
- The cardinality of a set is equal to the cardinality of a set , denoted , iff there exists a bijection from to .
- If there is an injection from to , the cardinality of is less than or the same as the cardinality of and we write . When and and have different cardinality, we say that the cardinality of is less than the cardinality of and write .
所以说,比较集合的基数(cardinality of set) 的大小最关键的步骤就在于找到一个集合 到另一个集合 的单射,如果这样的单射能够找到,就有 。
4.2. 可数的 Countable
- A set that is either 有限的(finite) or has the same cardinality as the set of positive integers called 可数的(countable).
- A set that is not countable is called 不可数的(uncountable).
- When an infinite set is countable, we denote the cardinality of by (阿列夫零(aleph null)).
- If , the set is 可数无穷(countable infinite).
(1) : (2) :沿着对角线取——TBD (3) : 证明:正有理数集 是可数的。
证明: 到 之间的实数集是不可数的。
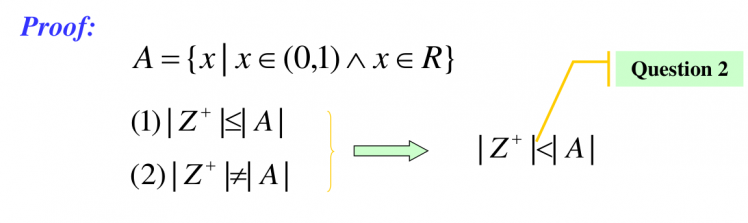
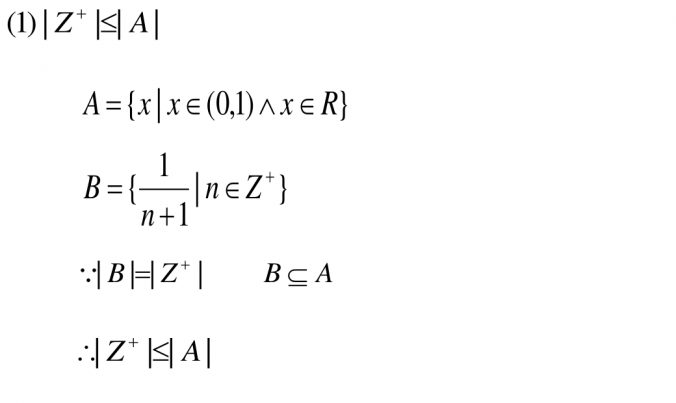

证明: 和 是等势的。

先直接给出一种数数方法:数集合的二进制表示。 再给出一个证明: 证明: 的所有有限子集是可数的。

4.3. 康托定理 Cantor's Theorem
The cardinality of the powerset of an arbitrary set has a greater cardinality than the original arbitrary set. 实际上有:。 Theorem: 康托定理(Cantor's Theorem)