本篇笔记介绍了时序电路的基本概念和分析方法,包括时序电路的分类(Mealy 型和 Moore 型)、离散事件模拟、锁存器和触发器的工作原理及其时序参数。详细讨论了锁存器的时序问题及其解决方案,触发器的标准符号和描述方法,以及时序电路的设计步骤和状态赋值方法。通过状态表和状态图的形式,帮助理解时序电路的行为和设计过程。(由 gpt-4o-mini 生成摘要)
1. 时序电路分析 Sequential Circuit Analysis
1.1. 时序电路介绍 Introduction to Sequential Circuit
我们将某一时刻存储存储元件(storage element) 中的二进制信息称为该时刻时序电路的状态(state)。
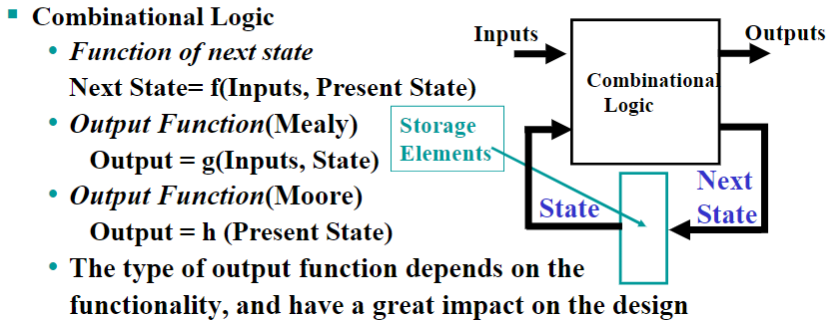
按照输出除了基于当前状态之外是否依赖于输入,可以将视时序电路分为:
- Mealy 型电路(Mealy model circuit):输出只和前一个状态有关
- Moore 型电路(Moore model circuit):输出和输入及当前输入有关
根据输入信号的时间和内部状态改变的时间,可以将时序电路分为:
- 同步时序电路(synchronous sequential circuit):
- 同步时序电路是通过时钟发生器(clock generator) 产生周期性的时钟脉冲(clock pulse) 来实现的。
- 把时钟脉冲作为存储元件输入信号的同步时序电路称为钟控时序电路(clocked sequential circuit)。
- 异步时序电路(asynchronous sequential circuit):
- Behavior defined by knowledge of inputs at any instant of time and the order in continuous time in which inputs change
- If clock is regarded as another input, all circuits are asynchronous!
- Nevertheless, the synchronous abstraction makes complex designs tractable!
1.2. 离散事件模拟 Discrete Event Simulation
可以通过离散事件模拟(discrete event simulation) 来更好的理解时序电路的时间行为。离散事件模拟的规则如下:

我们以一个二路选择器为例:
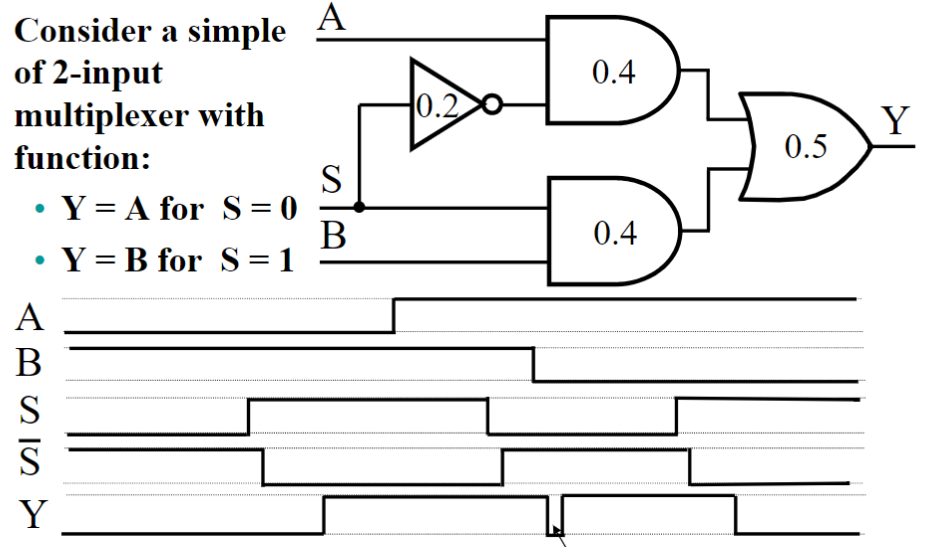
- 毛刺(glitch):或称瞬态错误。当 从 变为 时,由于非门有 0.2ns 的延迟,由
如果把选择器的输出 直接连到输入 上呢?
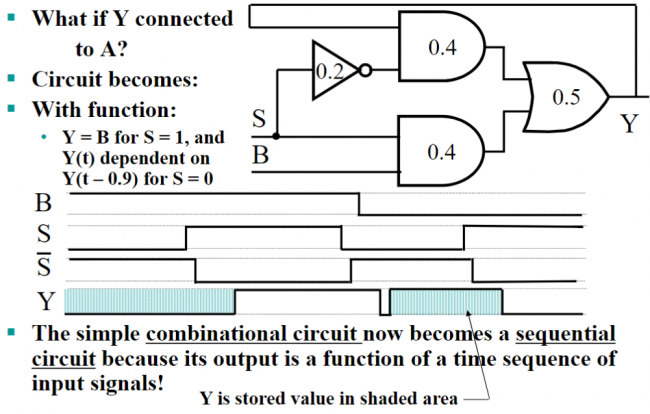
- 这里的 Y 不仅是输出,还可以记忆电路的状态(state)。
如果再多加一个反相器(inverter) 呢?
时钟发生器
2. 锁存器 Latchs
2.1. SR 锁存器与 S'R'锁存器 S-R Latch and - Latch
SR 锁存器通过两个或非门实现。
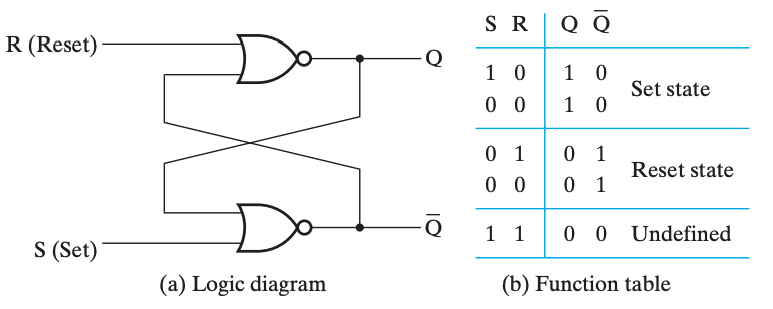
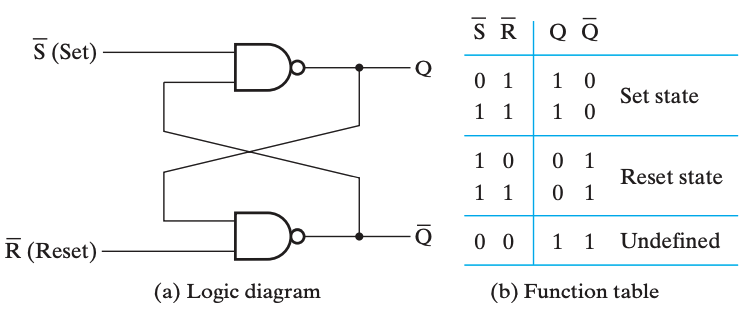
在 SR 锁存器中, 的输入是禁止的(forbidden) 或者说未定义的(undefined),此时输出端 和 同时成立。一般不使用这种状态。
S'R' 锁存器通过两个与非门实现。
-
S'R' 锁存器是 触发的,即 时将 置 ;而 SR 锁存器哈斯 触发的,即 时将 置 。不过从结果上来说,置为时 的值与 的值应相同。
-
如果 和 同时从 0 变成 1,则输出是不稳定的(unstable)。如果两个与非门的时延完全相同,则输出会在 01 之间震荡,否则会稳定在 或 中的一个状态,取决于两个与非门的时延。
2.2. 带时钟信号的 SR 锁存器 Clocked S-R Latch
多输入一路信号 与 信号作与或,这里 可以理解为 控制(control) 或时钟(clock)。只有 时输入才被接受; 时无论输入如何改变锁存器都为保持状态。

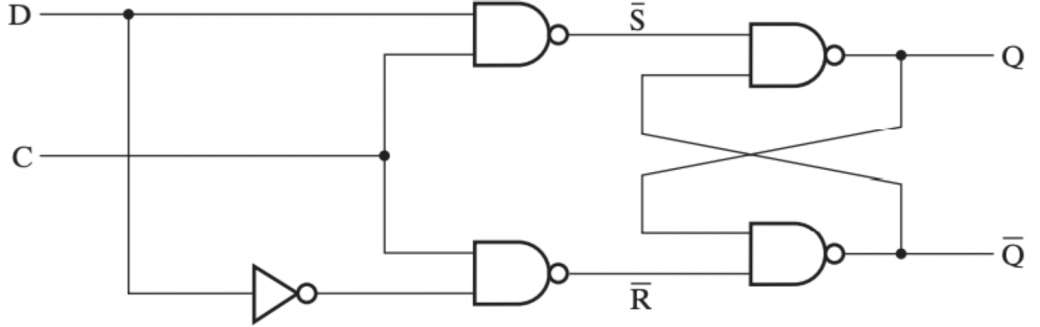
2.3. D 锁存器 D Latch
给 Clocked S-R Latch 添加一个反相器可以得到 D 锁存器(D latch),这样 的值和 的值一定相反,而我们通过控制信号 来控制是否应处于保持状态。当控制输入信号有效()时输出 会根据输入 的改变而改变,从这种意义上来讲,锁存器是透明(transparent) 的。
如果直接把输出 接到 上时,若 ,则 D 锁存器的值将不断跳变,这就是空翻问题。这主要是因为 D 锁存器的输入和输出是同时允许变化的(不是同时变化,是指在输出可以变化的时候输出也能变) 空翻的问题不光在 D 锁存器中存在,而是锁存器的普遍问题。 透明的问题——空翻(the latch timing problem)
| 描述 | |||
|---|---|---|---|
| 0 | X | 输出不改变 | |
| 1 | 0 | 0 | 复位 |
| 1 | 1 | 1 | 置位 |
2.4. 锁存器的时序问题 The Latch Timing Problem
锁存器存在锁存器的时序问题(the latch timing problem):在时钟脉冲有效()时,输入信号的改变随时会引起输出的改变,即上文所说的透明性。那么当时钟脉冲保持为 1 时,锁存器的输入信号可能因为其余锁存器的输出信号的改变而改变,从而在一个时钟周期内发多次变化,这是我们要引入触发器的原因。
如考虑这一电路中, 的时间内 的值会反复振荡,且最后结果不确定。而我们期望的功能时,一整段 只会导致 的值改变一次。
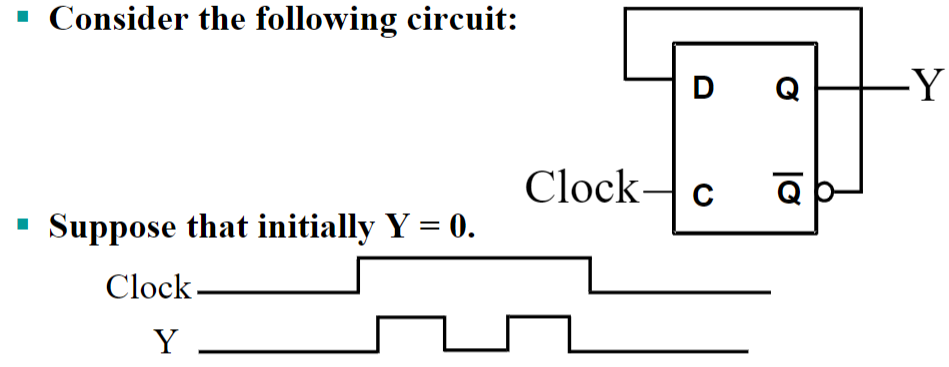
一种可行的解决方案是: 时(输入的时候)先不改变输出,等到 时在改变,这就是主从触发器的原理。
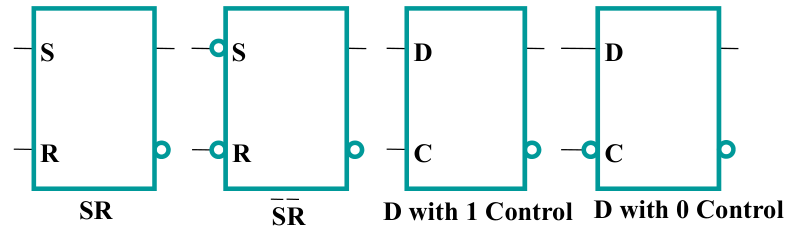
2.5. 锁存器的标准符号 Standard Symbols for Latches
3. 触发器 Flip-Flop
3.1. 主从触发器 Master-Slave Flip-Flop
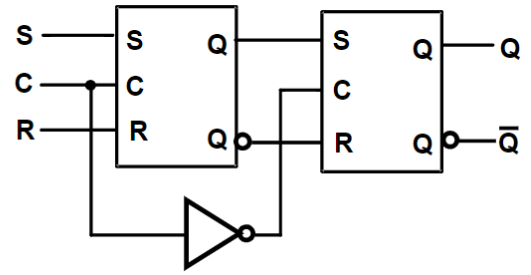
主从触发器(master-slave flip-flop) 一般通过将两个 SR 锁存器先后连接起来所得到,其中前者称为主锁存器(master latch),后者称为从锁存器(slave latch),两者的控制信号是相反的。
如果 时触发器的输入是 ,,但是由于电路问题出现了 或 的毛刺(glitch),就会改变主锁存器的值(而不是像期望的那样处于保持状态),并将这一有问题的修改在下一个时钟上升沿到来时传递给从锁存器。 为了避免发生一次性采样问题,主从触发器要求其的输入信号在半个时钟周期内不能改变(即 的时间内)。 主从触发器的缺憾——一次性采样问题(1s catching problem):
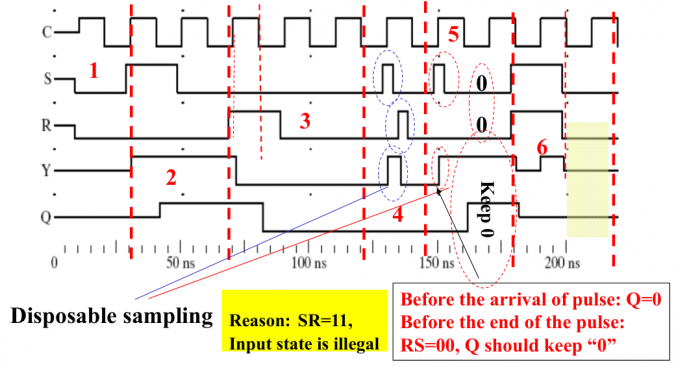
3.2. 边缘触发式触发器 Edge-Triggered Filp-Flop
边缘触发式(edge-triggered) 触发器忽略了保持阶段的时钟脉冲,只有在时钟信号发生跳变时(正边沿到来时或负边沿到来时)触发。
其逻辑结构可以看作把主从触发器中的主锁存器换成 D 锁存器,
3.3. JK 触发器 J-K Flip-Flop
| 描述 | |||
|---|---|---|---|
| 0 | 0 | 保持 | |
| 0 | 1 | 0 | 复位 |
| 1 | 0 | 1 | 设定 |
| 1 | 1 | 翻转 |
3.4. T 触发器 T Flip-Flop
| 描述 | ||
|---|---|---|
| 0 | 保持 | |
| 1 | 翻转 |
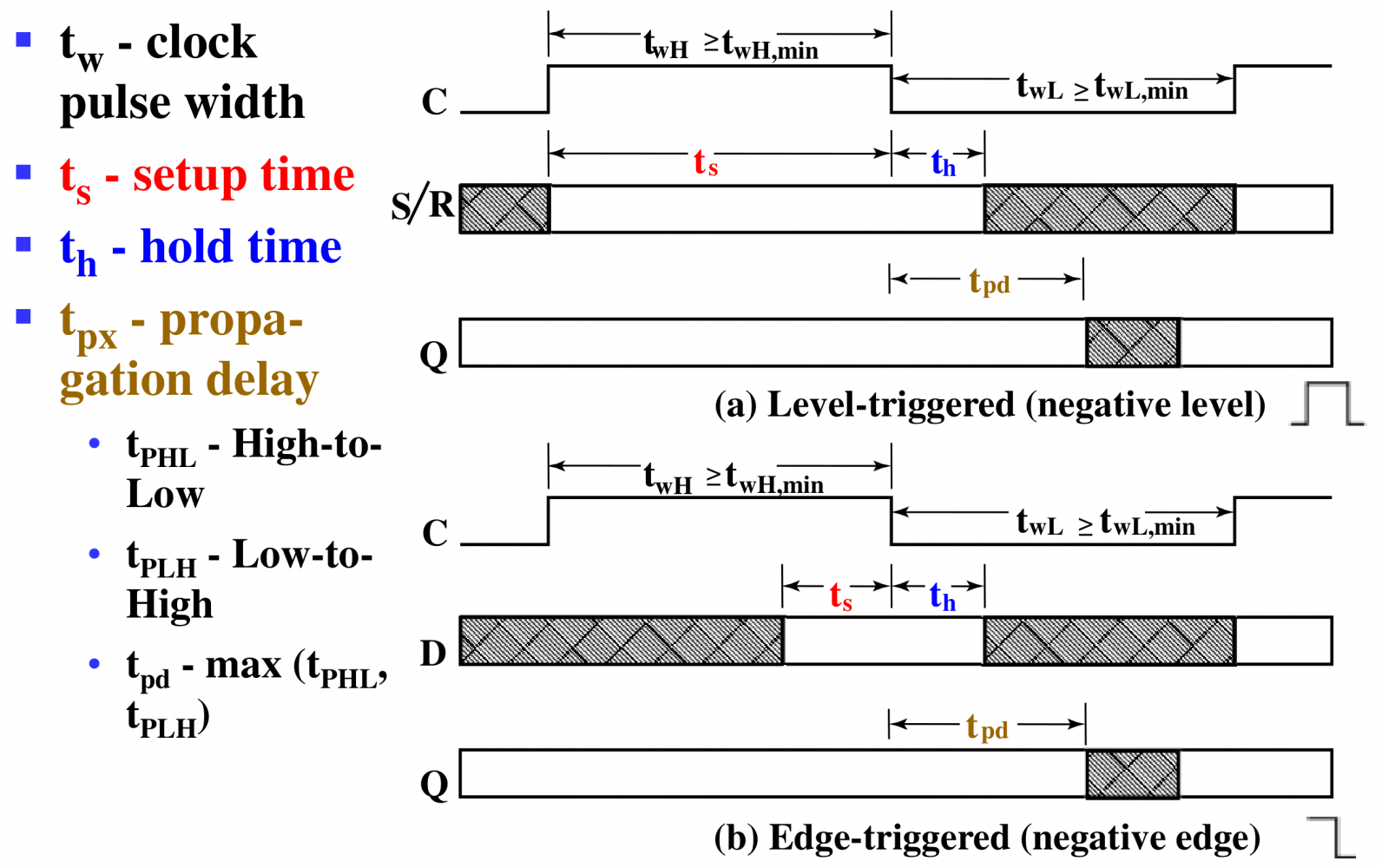
3.5. 触发器的时序参数 Flip-Flop Timing Parameters
- 建立时间(setup time):输入数据在时钟信号的上升沿或下降沿到来之前,需要保持稳定的时间。
- 对于主从触发器,为了避免一次性采样问题,其 setup time 应为半个时钟周期。即对于高电平激活的电路,其在时钟信号维持高电平期间不能改变输出。
- 对于边缘触发器,其所需要的 setup time 比主从触发器小很多,但也并不是 。
- 保持时间(hold time):输入数据在时钟信号的上升沿或下降沿到来之后,需要保持稳定的时间。
- 经常等于 ,即时钟脉冲之后对输入信号是否保持没有要求。

- 时钟脉冲宽度(clock pulse width):一个时钟周期中,时钟信号为高电平()或低电平()的时间。取决于触发器是在时钟信号的上升沿触发还是在时钟信号的下降沿触发。
- 传播延迟(propagation delay):从时钟信号的上升沿或下降沿(注意这里和组合电路中的定义略有不同)到触发器输出稳定,所需要的时间。其中
- 输出信号从高到低所需要的传播延迟定义为 ;
- 输出信号从低到高所需要的传播延迟定义为 。
两者可能不同。对触发器传播延迟的定义可取两者的最大值或平均值,如
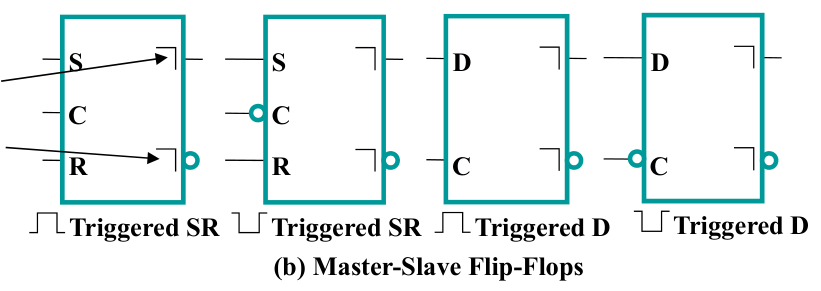
3.6. 触发器的标准符号 Standard Symbols for Flip-Flops
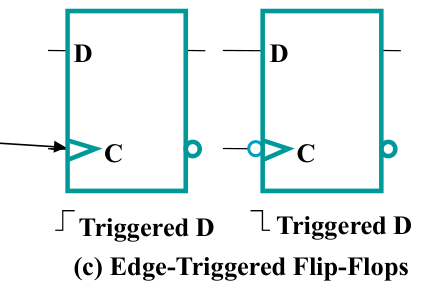
3.7. 触发器的描述方法
常用于分析(从当前状态和输入中得到下一状态):
- 特征表(characteristic table):定义了下一状态与当前状态和输入的关系。
- 特征方程(characteristic equation):用布尔函数来表示下一状态与当前状态和输入的关系。
常用于设计(从状态中得到输入):
- 激励表(excitation table):列出所有可能的当前状态和下一状态,从而确定输入。
4. 时序电路分析 Sequential Circuit Analysis
4.1. 整体模型 General Model
 整体模型
整体模型
对于一个输入为 ,输出为 ,状态为 的时序电路可以这样定义其:
- 输出方程(output function):。
- 触发器输入方程(flip-flop input equation):。
- 次态方程(next state function):。
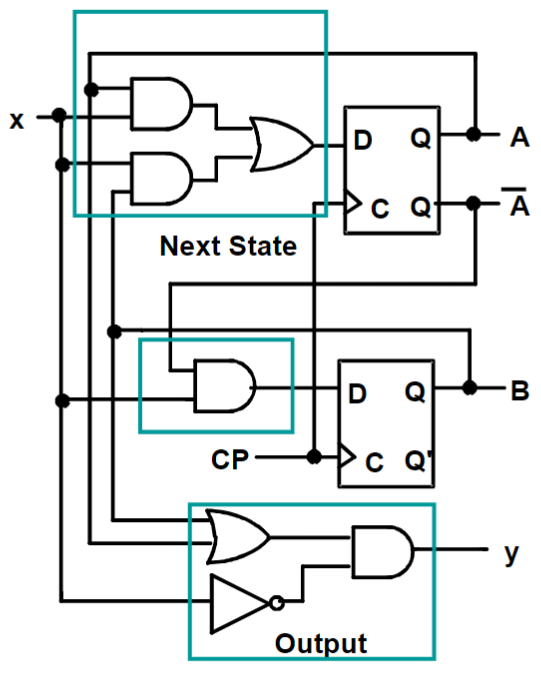 来自课本 Figure 5-15
来自课本 Figure 5-15
 时序电路分析过程
时序电路分析过程
4.2. 状态表 State Table
状态表(state table) 由四部分组成:当前状态(present state)、输入(input)、下一状态(next state) 和输出(output)。
这里我们不妨假设共有 个输入和 个触发器,则 Mealy 型电路的状态图可表示如下,共 行,对应着可能的所有输出。
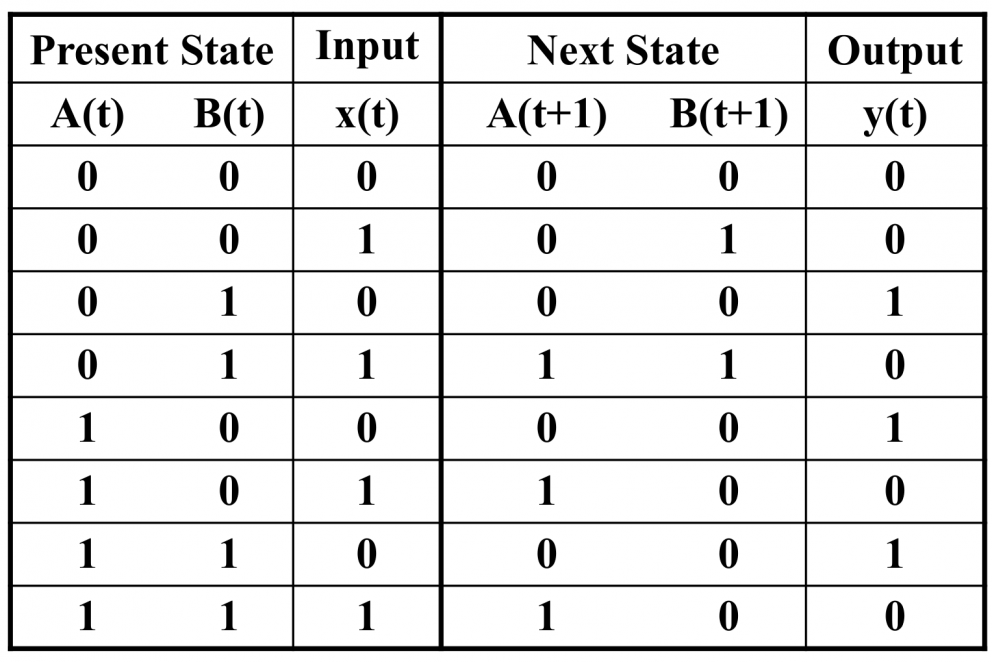 Mealy 型电路的状态表
Mealy 型电路的状态表
由于 Moore 型电路的输出只和当前状态有关,所以只需要 行即可,可以把 种不同输出所转移到的下一状态写到列上。
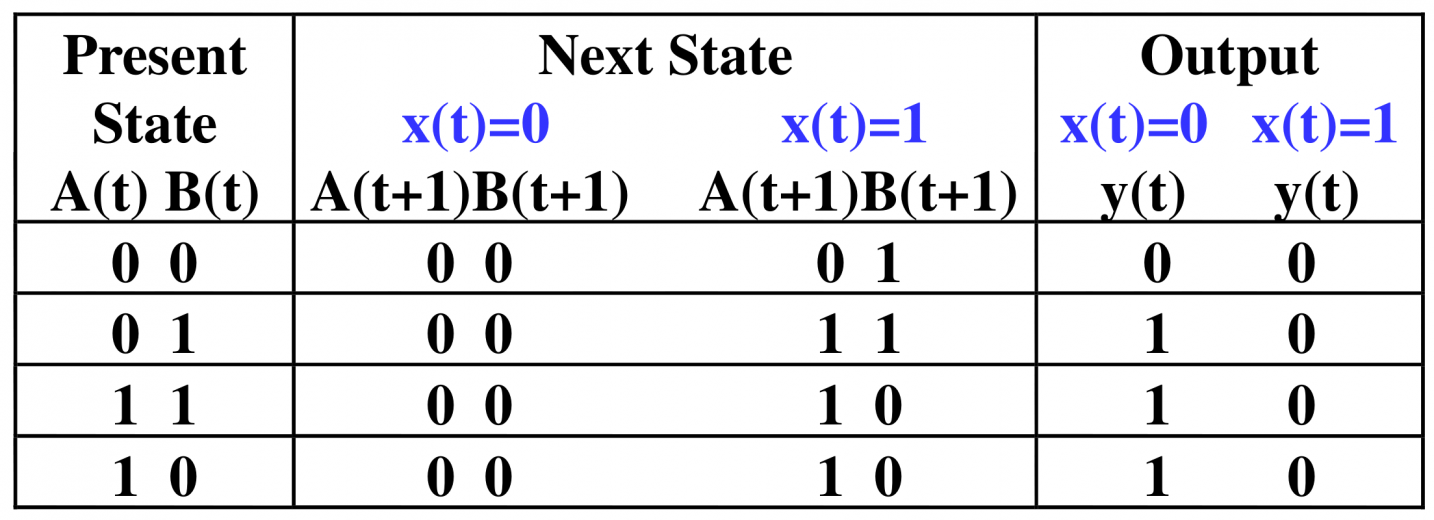 Moore 型电路的状态表
Moore 型电路的状态表
4.3. 激励表 Excitation Table
用当前状态和下一状态来描述输入(展示从当前状态转移到下一状态所需要的输入)。
4.4. 激励方程 Excitation Equation
4.5. 状态图 State Diagram

- 节点表示状态,边表示输入/输出(这一输入下会转移到的状态及对应的输出)
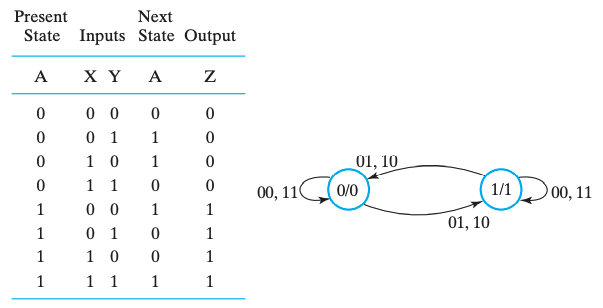
- 节点表示状态/输出,边表示输入(这一输入下会转移到的状态)
我们称呼两个状态是等价(equivalent) 的,当且仅当对于任意的输入序列,其输出序列都是相同的。如下面这个例子,
4.6. 状态机 State Machine Diagram
对于更复杂的逻辑,我们可能需要用状态机(state-maching diagram) 来表示。
听说考试没有考过?咕了咕了。
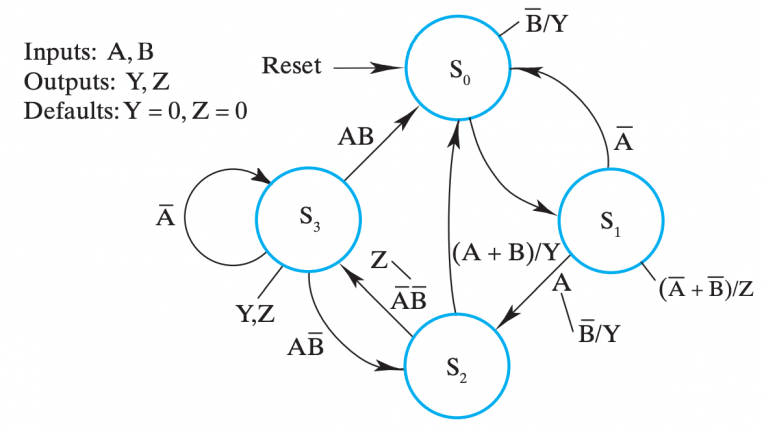
5. 延迟分析 Delay Analysis
注意 区分的是输出而不是输入。
6. 时序电路设计 Sequential Circuit Design
6.1. 设计步骤 The Design Procedure
- 确定系统的行为;
- 描述系统行为过程中,要注意状态的复用(不过并非状态越少成本就越小,这里有触发器数量和组合逻辑电路的 trade-off);
- 确定电路的初始状态(复位状态(reset state),通过给定复位(reset)信号实现);
- 复位一般可以是异步的;
- 阐述输入和输出之间的逻辑关系,并用真值表或逻辑表达式表达出来;
- 给设计好的状态编码赋值,得到具体的状态表;
- 我们可以使用 按计数顺序、 按格雷码、用独热码 来给状态赋值,更系统的方法比较复杂,不做讨论;
- 其中还有一种情况是所需要的状态不能完整填充 2𝑛2n 种情况,需要设计无效状态,这种时候可以不考虑它们;
- 根据状态表确定使用的触发器及其输入方程;
- 根据状态表确定输出方程;
- 优化输入方程和输出方程;
- 将优化后的逻辑设计工艺映射到硬件实现上;
- 验证正确性(在仿真环境中);
- 主要就是看能不能复现状态图;

6.2. 状态赋值 State Assignment
用 位二进制给 种状态各自分配一个不同的编码,需要使用 个触发器。剩余 个状态未使用,可视为不定项。
常见的状态赋值方法如下:
| 赋值方法 | 特性 |
|---|---|
| 按照计数的顺序(counting order) 分配 | |
| 按照格雷码顺序(Gray code order) 分配 | 在使用卡诺图作化简时非常方便 |
| 单热点(one-hot) 赋值 | 每个状态对应一个触发器,跳变最少效率最高 |