本篇笔记主要介绍了组合逻辑电路的基本概念，包括逻辑运算、逻辑门的类型及其特性、布尔代数的基本法则、规范形式以及卡诺图的使用方法。此外，还探讨了电路优化的目标和方法，帮助读者理解如何在设计中实现高效的逻辑电路。（由 gpt-4o-mini 生成摘要）

1. 逻辑和逻辑门 Binary Logic and Gates

1.1. Logical Operators

三种基本的逻辑运算(logical operator)：

• 和(and) is denoted by $\cdot$ or $\land$；
• 或(or) is denoted by $+$ or $\lor$；
• 非(not) is denoted by $\overline{\,\,}$ or $\sim$。

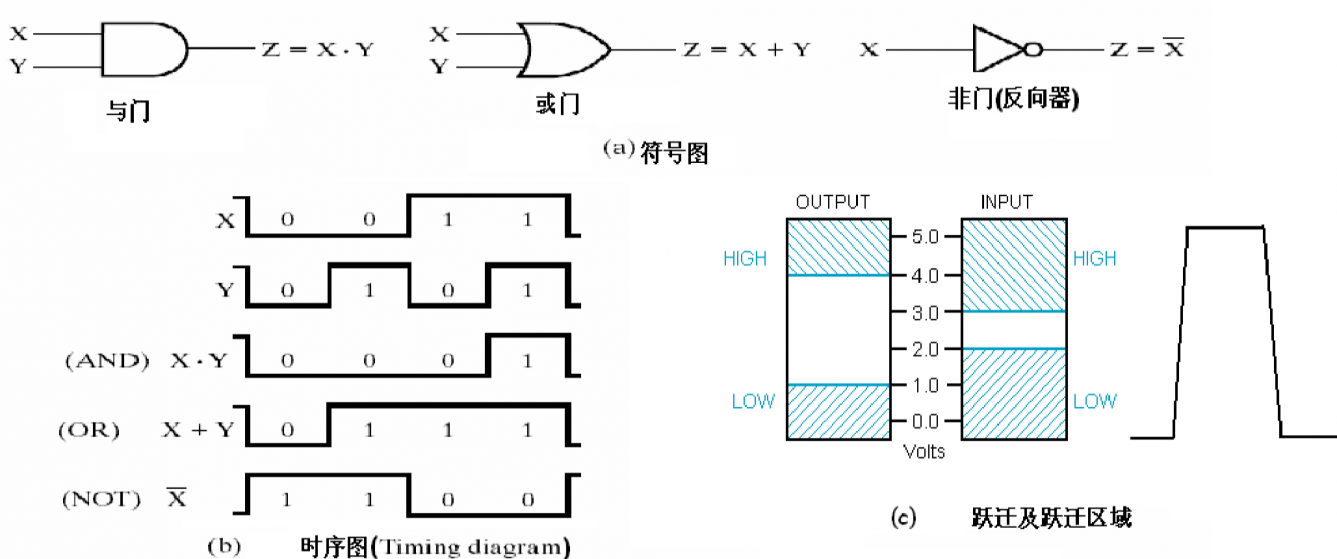认识基本的逻辑门

• 在与门和或门与线连接处画小圆圈可以表达非的意思。
• 逻辑门在从 01 直接跃迁时需要时间，在设计时序电路时可能需要考虑。

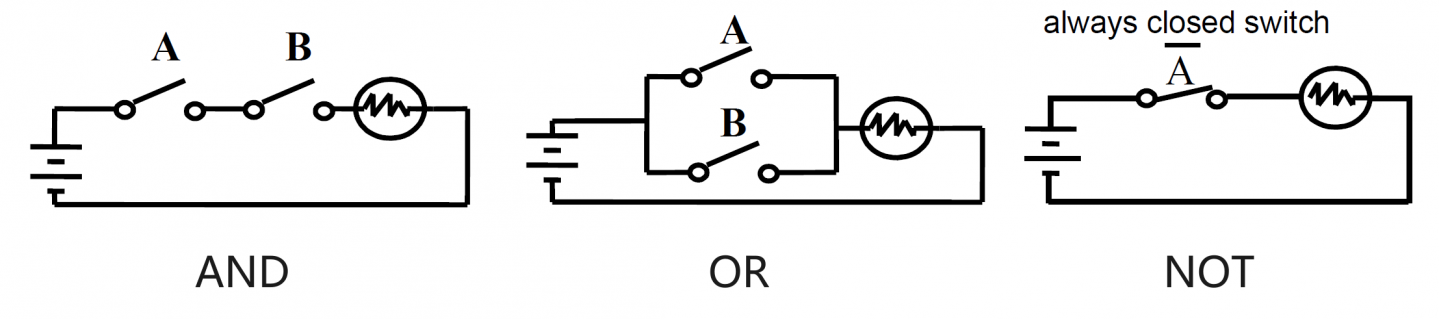用电路表示的逻辑运算

1.2. Logic Gates

逻辑门(logic gate) 是在硬件层面上实现布尔代数的逻辑单元。其操作对象为高低电平。但是由于是物理层面的实现，所以会有一些逻辑运算层面不会出现的问题，比如  延时(delay)。

一般来说，逻辑电路有 CMOS 和 TTL 两种：

1.2.1. CMOS Circuits

CMOS 工作原理

CMOS 电路实现的逻辑门

1.2.2. TTL Circuits

1.3. Universal Gates

NAND 和 NOR 门是通用门(universal gate)。

1.4. Additional Gates

2. Additional Gates and Circuits

2.1.1. NAND Gates

PROS:

• 是实现起来最简单最快的电路门。The NAND gate is the natural implementation for the simplest and fastest electronic circuits
• 是通用门——可以通过与非门的组合表示任意布尔运算。Universal gate - a gate type that can implement any Boolean function.

2.1.2. Buffer

缓冲器(buffer)：

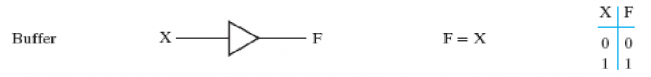
PROS:

• 可以抬高电路电压。A buffer is an electronic amplifier used to improve circuit voltage levels
• 可以加速电路操作。To increase the speed of circuit operation.

2.1.3. 3-State Buffer

三向缓冲器(3-state buffer)：除了输入和输出，它还有一个使能端(enable) 来控制输出。

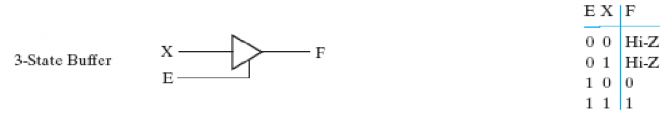
• Hi-Z 高阻态（可以理解为悬空）

3. 布尔代数 Boolean Algebra

3.1. 基本法则 Basic Laws

也可以考虑使用亦或(xor) 进行化简，因为亦或运算有很好的结合律。

3.2. 规范形式 Canonical Form

对于一个逻辑变量 $X_i$，我们称 $X_i$ 为它的 true form，$\overline{X_i}$ 为它的 complemented form。

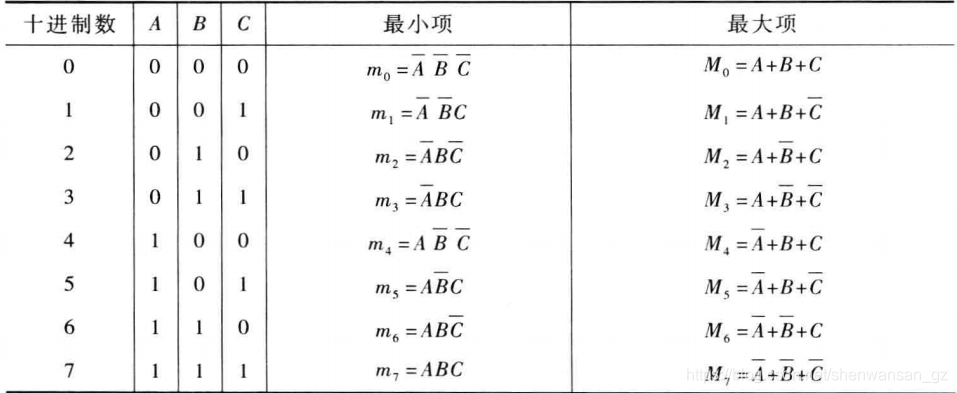
最小项(minterm)：Minterms are AND terms with every variable present just once in either true or complemented form.

• 所有 $n$ 个变量都需要出现在最小项中，一个最小项与真值表的一行相对应。
• 用 $m_i$ 表示第 $i$ 个最小项，如 $n=3$ 时 $m_0=\overline{ABC}$，$m_4=A\overline{BC}$。
• 对于一组变量的取值，只有一个最小项为 $1$。
• 任意两个最小项的积一定是 $0$：$m_i \cdot m_j = 0 \quad(i\neq j)$。
• 所有最小项的和为 $1$：$\displaystyle{\sum_{i=0}^{2^n-1} m_i} = 1$。
• 对于任意一个逻辑函数 $F$，$m_i$ 要么在 $F$ 的 DNF 中要么在 $\overline{F}$ 的 DNF 中。

最大项(maxterm)：Maxterms are OR terms with every variable appearing just once in true or complemented form.

• 用 $M_i$ 表示第 $i$ 个最小项，如 $n=3$ 时 $M_4 = \overline{A} + B + C$（注意这里对应 literal 的方式和最小项是相反的）。
• 对于一组变量的取值，只有一个最大项为 $0$。
• 任意两个最大项的和一定是 $1$：$M_i+M_j = 1 \quad (i\neq j)$。
• 所有最大项的积为 $0$：$\displaystyle{\prod_{i=0}^{2^n-1} M_i= 0}$。
• 对于任意一个逻辑函数 $F$，$M_i$ 要么在 $F$ 的 CNF 中要么在 $\overline{F}$ 的 CNF 中。

最小项之和(sum of minterm, SOM) 也被称为 DNF，最大项之积(product of maxterm, POM) 也被称为 CNF。所有命题函数都可以被化简成这种形式，这两种形式被称为规范形式(canonical form)。

3.3. 标准形式 Normal Form

可以通过卡诺图化简得到积之和(sum-of-product, SOP) 或和之积(product-of-sum)。

基于 SOP/POS（或者退一步的 SOM/POM）的电路被称为二级电路。二级电路与多级电路相比，好处是时延少，代价是使用的逻辑门多。

更多简化方法：

• “AND - OR” Simplification
• “OR - AND” Simplification

4. 卡诺图 Karnaugh Maps

4.1. 使用卡诺图化简 Simplifying using Karnaugh Maps

以利用三变量卡诺图(karnaugh map, K-map) 求 SOP 为例：将 F 所有为 1 的最小项填入表中，可以得到对应的卡诺图。如果要求 POS，则可先求 SOP，再应用一次德摩根定律转为 POS。

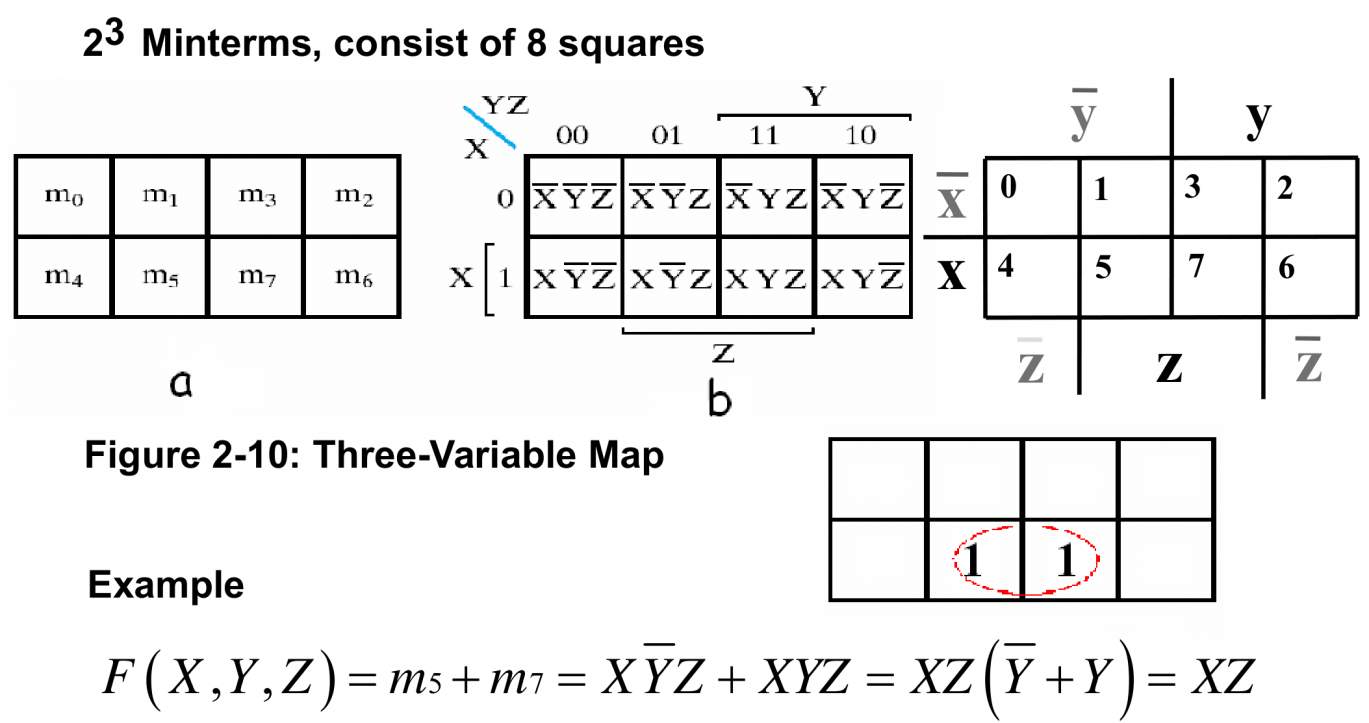
画完卡诺图后，我们需要分析其主蕴含项，即就是画尽可能大的框。

• 蕴含项(implicant)：对每一个最小项取值都为 1 的乘积项。对应卡诺图中全为 1 方格且大小为 2 的幂次的方框。
• 主蕴含项(prime implicant)：如果从蕴含项中移去任意一个变量，所得的乘积项就不是蕴含项，则称为质蕴含项。对应卡诺图中一个不能再向任何方向拓展的方框。
• 质主蕴含项(essential prime implicant)：如一个 1 方格仅存在于某个质蕴含项内，则称这样的主蕴含项是必要(essential) 的，称为质主蕴含项或必要主蕴含项。

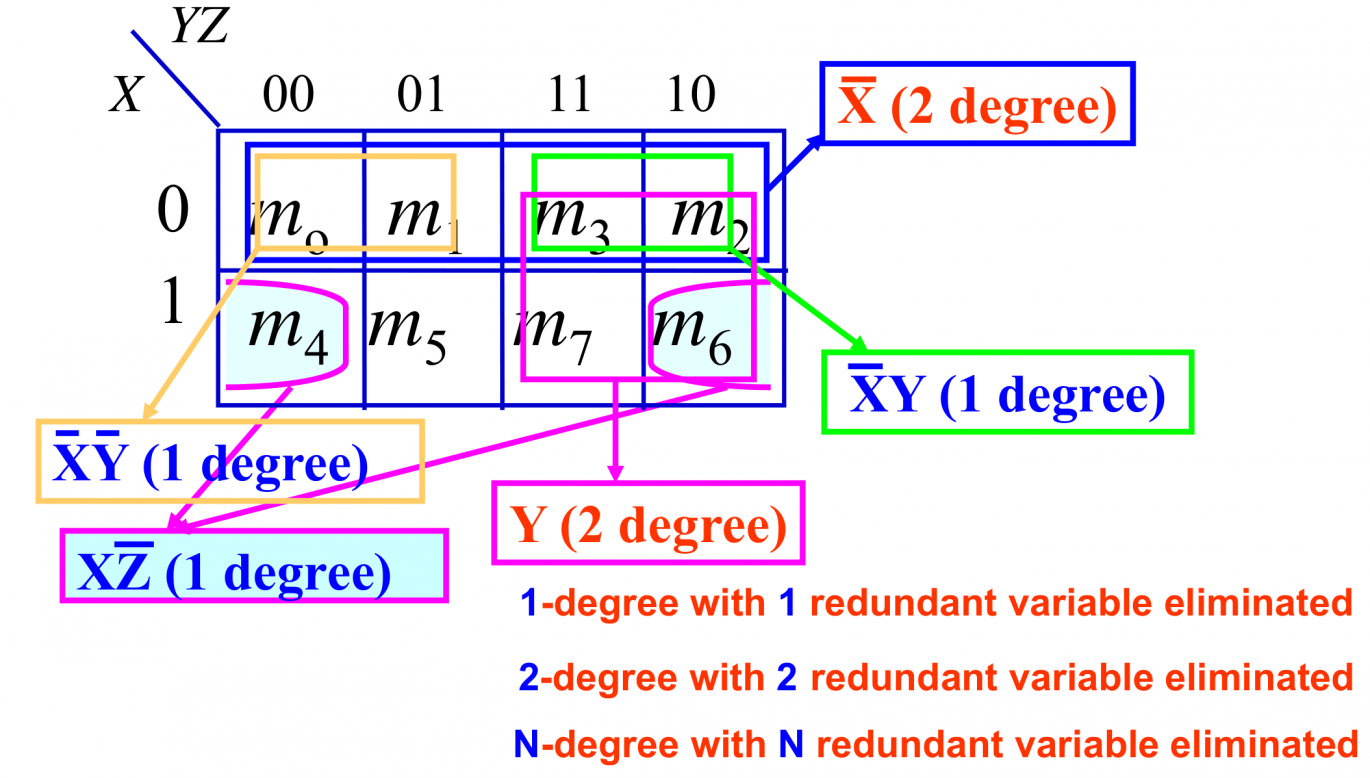
在使用卡诺图找到布尔函数的主蕴含项后，可以利用主蕴含项进行化简。可以先选择所有的质主蕴含项，再使用一些主蕴含项来覆盖未被覆盖的方格 1。所以优化后的最优结果可能不是唯一的。有一些细节需要注意：

• 找主蕴含项时，不要忘了考虑跨越边界而联通的情况。如果最后选到了一个非主蕴含项，那么这一优化结果一定不是最优的。
• 选择多个主蕴含项时，相互之间可以重叠，注意电路优化的目标减少代价。

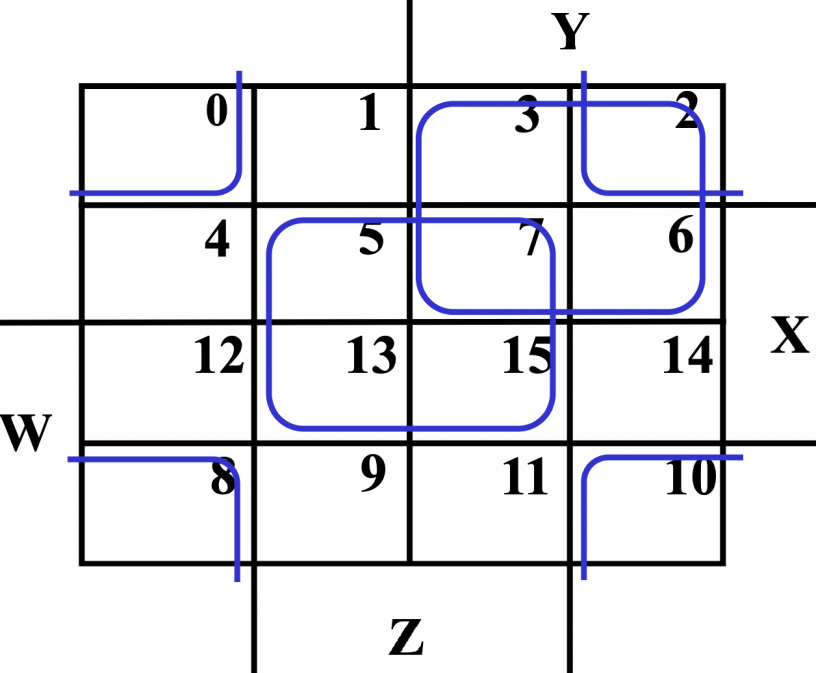
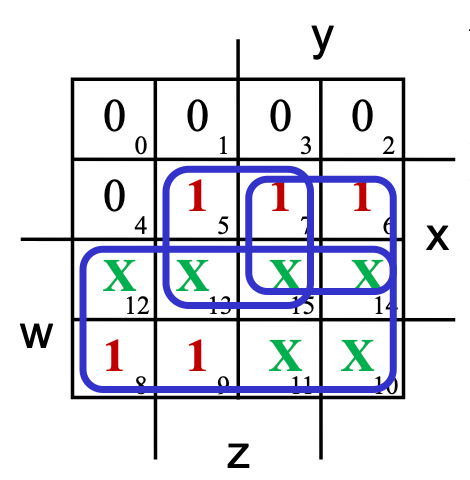
4.2. 不定项 Don’t Care Conditions

不定项(don't-care condition) 是指电路优化过程中，没有给出定义的项，他们可能是：

• 输入组合不会出现；
• 输入组合的输出不被使用；

对于这种项，在卡诺图中用 X 来表示，在最小项之和中用 $\sum d(\ldots)$ 表示。我们可以随意定义它们的输出，此时就可以利用这些项来方便我们的优化——当我们画出来的极大矩阵越大，成本就越低。

5. 电路优化 Circuit Optimization

电路优化(circuit optimization) 的目标是在找到给定成本计算方式下的最优电路。

• Literal Cost(L)：the number of literal appearances in a Boolean expression corresponding to the logic circuit diagram
• 门输入代价(gate input cost)(G)：the number of inputs to the gates in the implementation corresponding exactly to the given equation or equations.
• 带非门的门输入代价(gate input cost with NOTs, GN): G with inverters counted

一般来说，成本函数是一个关于 $\text{L, G, GN}$ 的函数。