本篇笔记概述了经典算法的多种类型,包括倒排索引、回溯算法、分治法、动态规划、贪心算法、近似算法、局部搜索、随机化算法、并行算法以及外部排序。每种算法都配有具体的例子和复杂度分析,帮助读者理解其应用场景和实现方式。通过这些内容,读者可以掌握算法设计的基本思想和技巧,为解决实际问题提供理论基础和实践指导。(由 gpt-4o-mini 生成摘要)
1. 倒排索引 Inverted File Index
1.1. Optimize a Search Engine
读取时的处理:
- word stemming
- stop words
阈值(thresholding):
- document: 只检索前面 个按权重排序的文档
- query:把带查询的 terms 按照出现的频率升序排序
搜索引擎的相关性度量(relevance measurement):
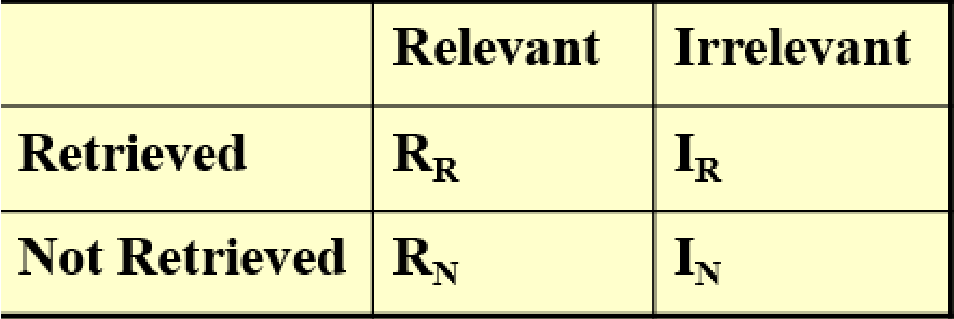
- 准确率(precision):指检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率 。
- 召回率(recall):指检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率 。
2. 回溯 Backtracing
- 解空间约束
求解问题的一个可靠方法是找出所有可能得情况,逐一检查,找到正确答案。回溯(backtracing) 算法利用了剪枝(pruning) ,可以减少对大量已知不可能的情况的显示检查。
- 尽量选择从少到多的搜索方式,这样在剪枝的时候可以一次性剪掉更多的情况数。
2.1. Minimax Search & α-β Pruning
定义 goodness 函数为 ,则 Human 想要最小化 而 Computer 想要最大化 。
剪枝的核心思想:根据当前局面可以推定不会影响上层节点结果的就可以进行剪枝。
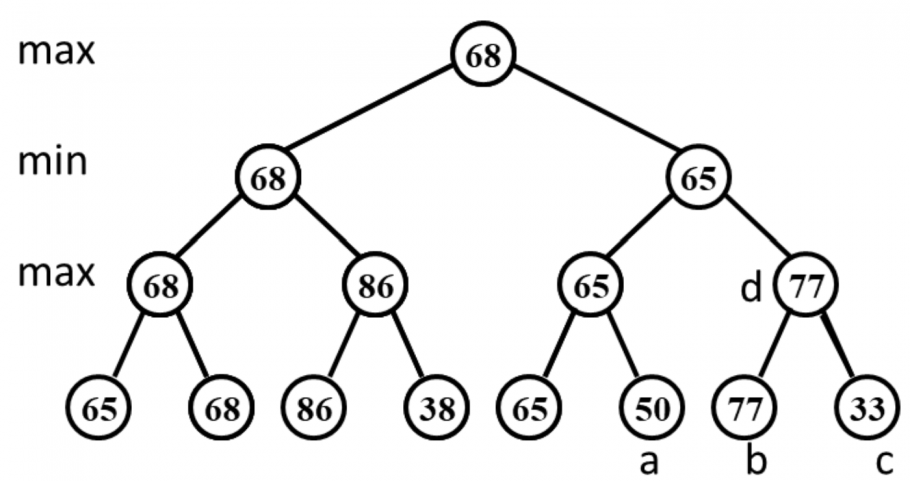
Given the following game tree, which node in the right subtree is the first node to be pruned with α-β pruning algorithm?
D。可以分析而知:无论节点 的值是多少,都不会影响到根节点 的值,故可以进行剪枝。 另外左子树中可以减掉的节点是 。 习题
答案
2.2. Examples
(八皇后问题)在棋盘中找到八个位置放置皇后,使得它们都不同行且不同列,也不能同时位于对角线上。 Eight Queens
在游戏树上进行 DFS 搜索。
在一条直线上找到 个地方建立加油站,已知它们两两之间的距离(共 对),求出所有加油站的位置,假定第一个加油站的坐标是 。 Turnpike Reconstruction Problem
就是暴搜。在 DFS 过程中维护未分配的距离集合,还有当前的处理区间,每次从距离集合中找到最大的距离 ,看新的加油站应当放在 的位置还是 的位置即可。
给一个从若干根长度为 的大棍子里切出来的小棍子长度集合,求最小的可能的 。 Stick Problem
从小到大枚举 然后将原来通过回溯法进行搜索。
经典井字棋小游戏。 Tic-tac-toe Game (play with computer)
这里定义 为 Player 能够赢得胜利的可能数(如果把剩下所有各自都填上你的棋子,可以有多少个三连),可以一定程度上表征局面对于自己的优劣情况。定义 goodness 函数 ,使用 Minimax 搜索交替进行选手——计算机的对弈,需要使用 剪枝。
3. 分治 Divide & Conquer
- 分治(divide conquer)
3.1. Complexity Analysis
分析分治算法的复杂度有三种常用的方法:
- 代换法(substitution method):先猜对答案,然后使用数归证明。
- 递归树法(recursion-tree method):写成多叉线段树的形式,每一层分别计算,最后加起来。
- 主方法(master method):用主定理解决。
3.2. Master Theorems
主定理(master theorems)


For each of the following recurrences, choose the one that we cannot apply the Master Theorems to solve. A. B. C. D.
AC?然而 pta 上的答案是 A。 习题
答案
3.3. Examples
给平面上 个点,求解最近点对。 Closest Point Problem
4. 动态规划 Dynamic Programming
- 背包问题(the knapsack problem)
4.1. Examples
,求解 。 Fibonacci Numbers
两种实现:启发式搜索或者直接序列 DP,都是用一张表来存 。
安排 个矩阵的乘法的计算顺序,最小化计算量。(第 个矩阵 的大小是 ) Ordering Matrix Multiplications
区间 DP,。
给 个词的搜索频率,应如何构建 BST 以最小化 access 期望代价?相比于 Haffman 编码问题,我们确定了中序遍历,且内部节点上也能有键值。 Optimal Binary Search Tree
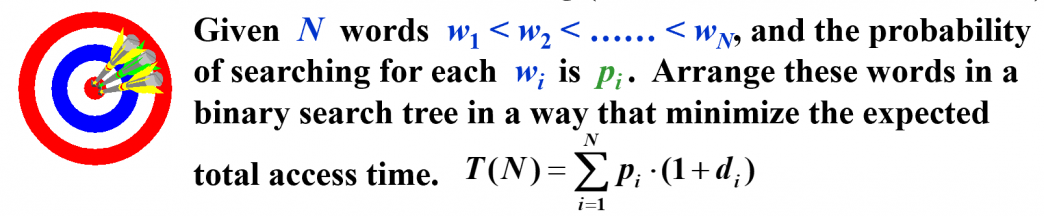
从最优子结构转移:最优方案的两棵子树一定是最优方案。定义 , 表示给区间 节点建树的最小花费,则有转移:
求任意两点间最短路径。 All-Pairs Shortest Path
我看了看怎么感觉就是 Floyd 啊?
有 步的工序,可以在两条生产线之间切换,消耗的时间和本次及上千次在哪条生产线完成有关,求最优生产流程。 Product Assembly

我看了看怎么感觉就是直接 DP 啊?
5. 贪心 Greedy
5.1. Examples
Activity Selection Problem

DP 做法:设 表示前 个单位时间里最多选几个,找到所有 的活动,从 转移。时间复杂度 ,不够优秀。
贪心做法:把所有区间按照右端点排序,每次取右端点最小的,即选择尽早结束的活动(反过来也可,即选择最迟开始的活动),然后把有重合的都删掉,如此循环直到结束。时间复杂度 。
哈夫曼编码问题。 Huffman Codes
建 Huffman 树的过程正体现了贪心思想。
6. 近似 Approximation
6.1. Approximation Ratio
设 为我们算法的 cost, 为最优解的 cost,定义近似率(approximation ratio) 为:
- 称这样的算法为 -approximation algorithm
- approximation scheme: 近似率 的算法,即 -approximation algorithm
PTAS:polynomial-time approximation scheme 关于 成多项式复杂度的算法 (设 为常数)FPTAS:fully polynomial-time approximation scheme 关于 和 都成多项式复杂度的 算法
6.2. On-line & Off-line Algorithms
在读入数据的时候进行决策,一旦决策之后不能修改。
6.3. Examples
Given items of sizes , such that for all . Pack these items in the fewest number of bins, each of which has unit capacity. ——这一问题是 NP-Hard 的。 Approximate Bin Packing
Next Fit 做法:依次读入每个物品,看看是否能和前一个物品放在同一个 bin,如果不行的话就开一个新 bin。
设用 Next Fit 做法生成的解为 (或 ),那么有 ,故 ,故至少需要 个 bin。 证明:设最优解为 ,则用 Next Fit 做法得到的解不超过 。
First Fit 做法:依次读入每个物品,扫描所有已有的箱子,找到第一个能放下的放,如果不存在则新开一个箱子放。设最优解为 ,则得到的解不超过 。
Best Fit 做法:依次读入每个物品,在可以放下这一物品的箱子中选剩余空间最小的,如果不存在则新开一个箱子放。设最优解为 ,则得到的解不超过 。
这里的 Next Fit、First Fit 和 Best Fit 做法都是在线做法,如果允许离线,则可将所有物品按照体积从大到小排序,然后应用 First Fit(或 Best Fit)做法。设最优解为 ,则得到的解不超过 。
就是 0-1 背包问题。 The Knapsack Problem (0-1 Version)
- 用 DP 解决的复杂度是指数级的,因为物品大小和 不同阶,实际上 Knapsack 问题是 NP-Hard 问题,Knapsack 的判定是 NPC 问题。
- 如果将物品的大小缩放到 的范围,则有多项式复杂度的 DP,但算法也变成了近似算法。
如果使用贪心做法,每次选(可选的)里价值最高或性价比最高的(两种做法分别做一次),可以证明近似比为 。
这里 是两种贪心做法得到结果的 max。 证明:贪心做法的近似比为 。
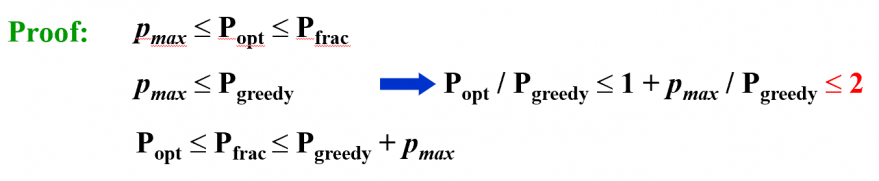

平面上给定 个点,确定 个圆心的位置覆盖所有点并使最大圆的半径最小。 The K-center Problem

若 K-center 存在 -approximation,则可用于精确求解 Dominating Set 问题,而后者是一个 NPC 问题。 定理:除非 ,否则不存在 的解法。
7. 局部搜索 Local Search
- : 是 的一个相邻解(neighboring solution),只需要对 进行一个微小的修改就可以得到。
- : 的邻域(nerghborhood),即 。
- 称 是 的 local optimum,即 且是其中最优的。
7.1. Gradient Descent
爬山——梯度下降法:每次在邻域中选一个最优的转移,如果找不到则退出。
容易陷入局部最优解中。
7.2. The Metropolis Algorithm
模拟退火——Metropolis 算法:每次在邻域中随机选一个转移,如果比当前情况更有则以一定概率 接收,否则概率接收且这一概率随迭代次数指数下降。
7.3. Examples
最小点覆盖问题。 Vertex Cover Problem
直接使用爬山问题容易陷在 e 局部最优解,建议使用模拟退火算法。
给定 其中边权有正负,给每个节点分配一个 ,称一个点是 state assignment 当且仅当 Hopfield Neural Network


state-flipping 算法:每次反转一个不稳定的节点作为转移。
证明:State-flipping 算法一定能达到一个稳定状态,且最多反转 次。

最大割问题。把点集划分为两部分 ,最大化 。 Maximal Cut Problem
采用类似于上一问的转移,即翻转一个点的状态。若进行爬山算法,可以得到一局部最优解 。设最优解为 。
证明:。

big-improvement-flip 算法:当新的局部最优解的增长的幅度小于 的时候就停止,这样算法可以在一定近似比的代价下保证在多项式复杂度内结束。
这样就有 ,可以在最多 次翻转后结束。 定理
8. 随机化 Randomize
有两种随机算法:
- 有非常高的概率给出正确答案。efficient randomized algorithms that only need to yield the correct answer with high probability
- 总是正确的,并在期望中运行的很有效率。 randomized algorithms that are always correct, and run efficiently in expectation
8.1. Random Shuffle
给每个元素分配一个随机的 key:a[i].key = rng() % (n * n * n),然后根据 key 进行排序。根据生日碰撞,这里取 作为模数就能有一个不错的效果。
8.2. Examples
总花费 = 面试次数 每次面试的花费 雇佣人数 雇佣费用。 The Hiring Problem
一种简单的做法:看到比先前更好的人就雇佣,但是在面试者按照优秀程度递增顺序进来的时候就会爆炸。不妨进行随机排序,则期望花费为 。
将前面的问题改为在线,但只能雇佣一次。 Online Hiring Problem - Hire at Once
一种较高概率成功的解:先面试前 个人但一定不从中雇佣,然后依次面试第 个人,其中第一个满足比前 个人优秀即 的人进行雇佣。可以证明取 时最优。
根据微积分的知识我们有: 那么取到最优解的概率为: 根据高中数学的知识可以知道取 时最大即 ,且概率为 。 证明:最优解 。
众所周知,直接选中间位置作为 pivot 的快速排序是可以被卡到 的,那应该怎么选呢。 Quicksort
随机一个数作为 pivot,但如果这一 pivot 是最小的 1/4 或最大的 1/4 则重选,期望意义下只重选一次。
这样至少会将规模划分为 和 ,可以证明复杂度是 。
9. 并行算法 Parallel Algorithm
两个模型:Parallel Random Access Machine (PRAM);Work-Depth (WD)。
9.1. PRAM Model

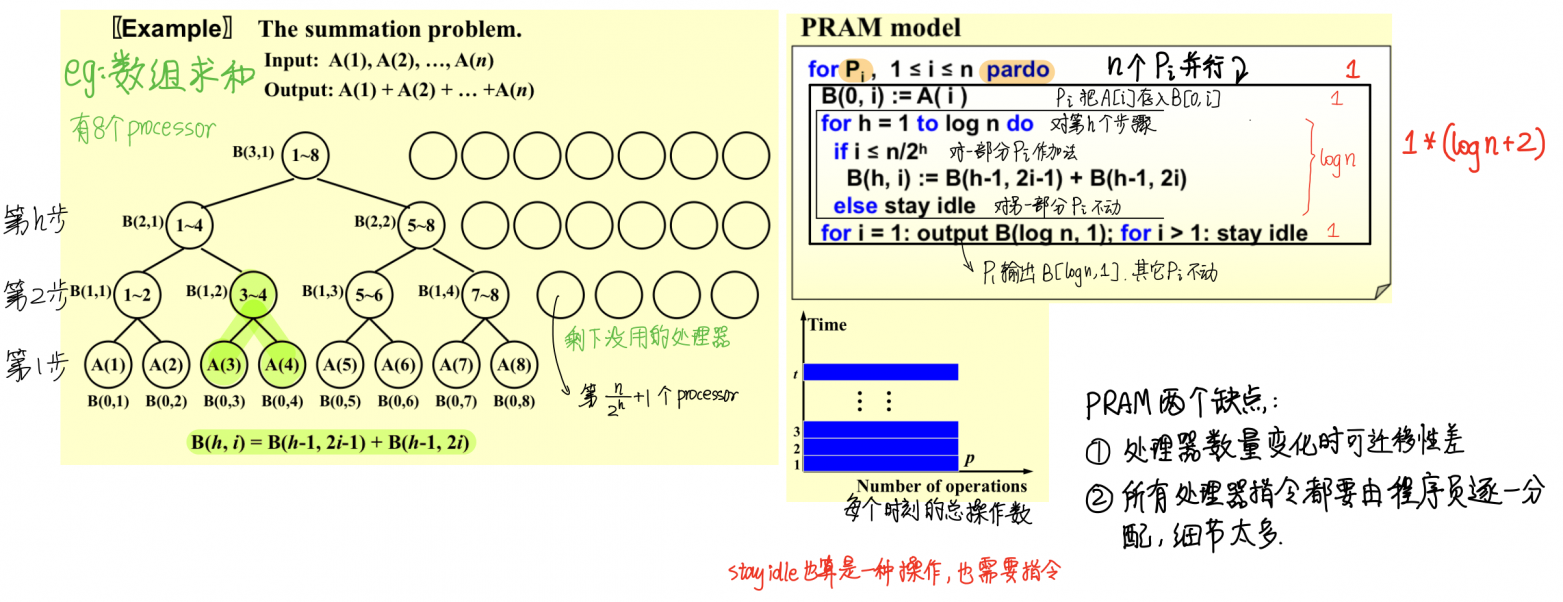
9.2. WD Model
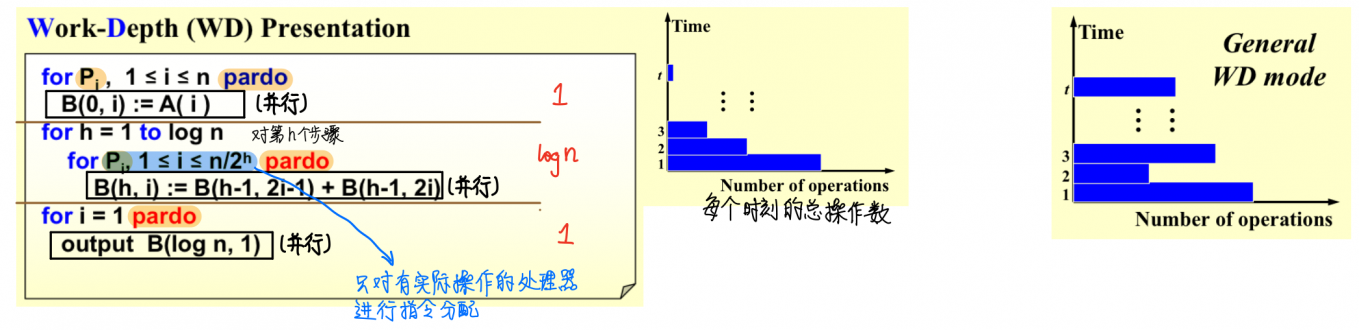
【WD-presentation Sufficiently Theorem】An algorithm in the WD mode can be implememnt by any processors within time, using the same concurrent-write convention as in the WD presentation.
找 个数的最大值,并行算法。 Maximal Finding
- Replace "+" by "max" in the summation algorithm.
- Compare al pairs (find ).
- Doubly-logarithmic Paradigm: Parition by .
- Paritition by .
- Random Sampling. . .
10. 外部排序 External Sorting
我们只有有限的内存(只能存放 个数)和若干 tape(一种特殊的存储结构,只能顺序读写),需要解决排序问题。
这个具体的过程特别抽象我懒得记录了,可以看一下别人的笔记。不过别因为这个是最后一讲就不看了,似乎是每年必考的内容。