本篇笔记主要介绍了可并堆的概念及其相关操作,包括左倾堆、斜堆和二项堆的定义、操作及复杂度分析。左倾堆通过空路径长度来定义节点的结构,斜堆则通过自适应的方式进行合并,而二项堆则是由多个堆有序树组成的森林。每种堆的合并、插入和删除操作都有其独特的实现方式和复杂度分析。(由 gpt-4o-mini 生成摘要)
1. Leftist Heap
空路径长度(null path length): 定义为从节点 任意没有两个孩子的子节点的最短距离。特别地,定义 ,对于叶子节点或只有一个孩子的子节点,其 显然为 。显然有:
左倾堆(leftist heap):对于左倾堆的每个节点,其左节点的 值大于等于右节点的 值。
1.1. Operations
1.1.1. Merge
递归合并,每次插入到右侧。插入后如果右子树的 更大则交换左右子树。
也有一种不“交换”左右孩子的方法,定义一个 函数每次根据左右孩子的 返回 较小的店作为右节点即可。
1.1.2. Insert
看做与一个单节点的子树合并。
1.1.3. DeleteMin
删去根,合并根节点的两个子树。
1.2. Complexity Analysis
TBD
2. Skew Heap
斜堆(Skew Heap),也叫做自适应堆(self-adjusting heap) 是另一种可并堆,它不需要记录任意一个节点的距离,只是在合并操作上有所改变。
2.1. Operations
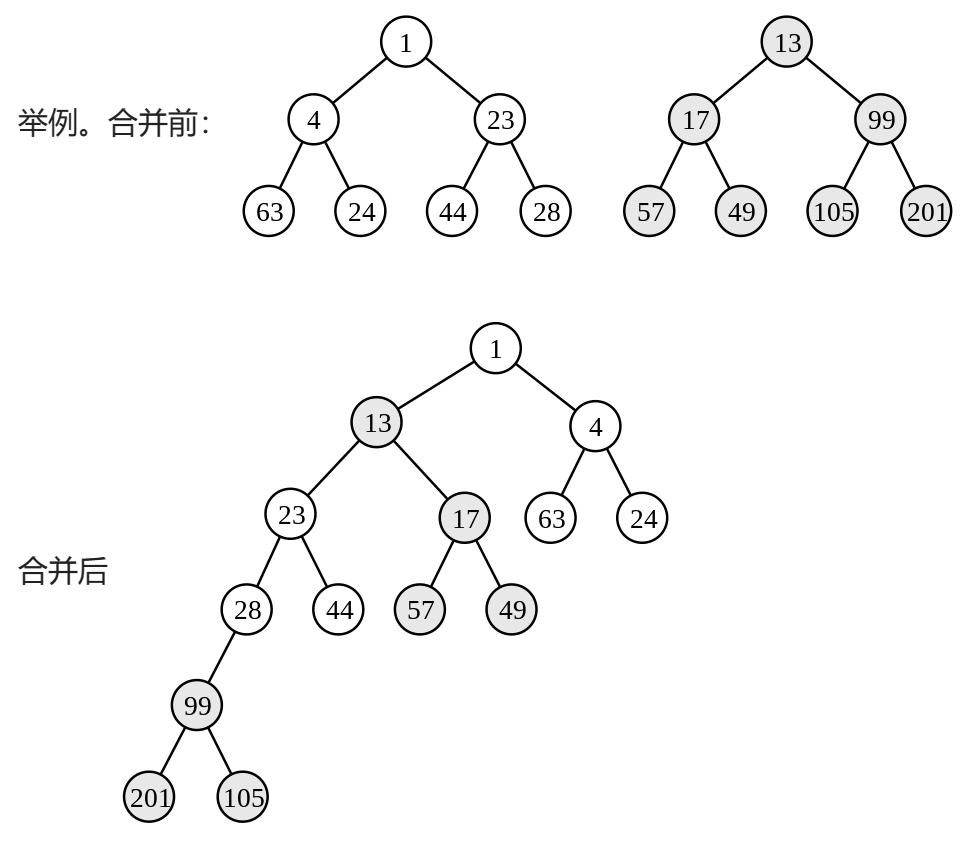
2.1.1. Merge (Recursive)
- 比较两个堆;设 是具有更小的 的键值的堆, 是另一个堆, 是合并后的结果堆。
- 根据堆性质,选 的根节点作为 的根节点。
- 令 的右子树为 的左子树。
- 令 的左子树为 的右子树与 合并的结果。
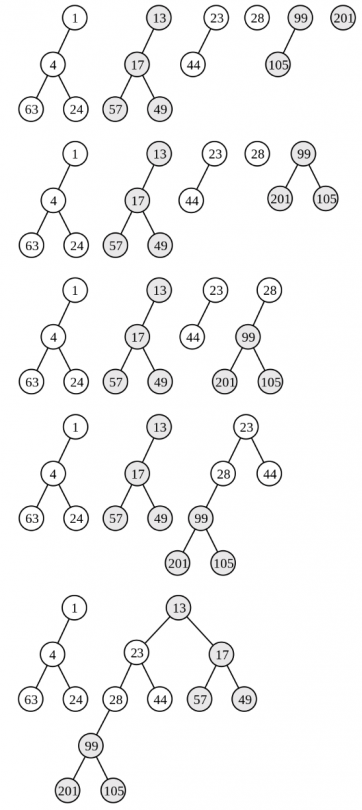
2.1.2. Merge (Non-recursive)
- 把每个堆的每棵(递归意义下)最右子树切下来。这使得得到的每棵树的右子树均为空。
- 按 的键值的升序排列这些树。
- 迭代合并具有最大 键值的两棵树:
- 具有次大 键值的树的右子树必定为空。把其左子树与右子树交换。现在该树的左子树为空。
- 具有最大 键值的树作为具有次大 键值树的左子树。
2.2. Complexity Analysis
重节点(heavy node):称一个节点 是 heavy 的,当且仅当它右子树的节点数大于等于左子树的节点数。
进行均摊分析,定义势能函数
考虑第 次合并过程,它们右路径上的轻重节点个数分别为 和 。则一次合并的实际代价为
另外注意到,一次操作后,重节点一定变成轻节点,但是轻节点不一定变成重节点。这是因为
- 对于一个重节点,原先较大的右子树交换到右侧且会与另一棵树合并,从而变得更大,故重节点合并后一定变成轻节点。
- 对于一个轻节点,虽然较重的子树被换到右侧,但是由于左子树和另一个树合并可能变得更大,故合并后有可能是轻节点也有可能是重节点。
故势能增加量
而右路径上的轻节点的数是 级别的,所以总复杂度为 。
3. Binomial Queue
二项堆(binomial queue):A binomial queue is not a heap-ordered tree, but rather a collection of heap-ordered trees, known as a forest. Each heap-ordered tree is a binomial tree.
二项树(binomial tree):A binomial tree of height is a one-node tree. A binomial tree, , of height is formed by attaching a binomial tree, , to the root of another binomial tree, .
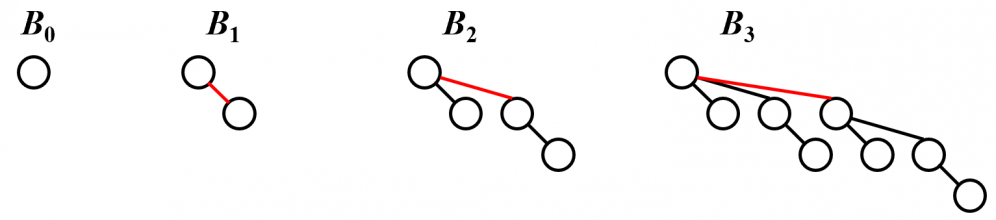
consists of a root with children, which are . has exactly nodes. The number of nodes at depth is . Observation
注意到二项树有以下重要性质:
- 二项树 的总结点数是 ,这意味着我们想要构建一颗大小为 的二项堆时,可以对 进行二进制拆分。
- 二项树的合并是简单的,可以通过两个 通过 的复杂度直接得到 ,并且维持堆性质不变。
3.1. Operations
3.1.1. FindMin
枚举 binomal queue 中的每个堆,取他们的根节点的最小值。由于 binomal queue 中的堆的数量是 的,故这一操作的复杂度为 。
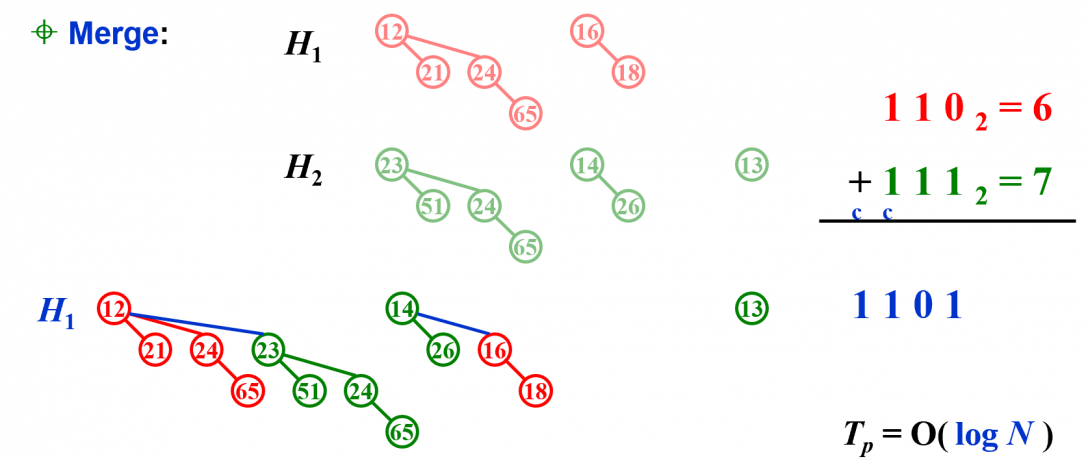
3.1.2. Merge / Insert
可以类比二进制数的竖式加法,来确定需要按照什么样的顺序将哪些 binomal trees 合并,这里别忘了要考虑进位。
3.1.3. DeleteMin
找到根节点值最小的 binomal tree,设为 将其根节点删除,其孩子应分别为 ,将这些孩子视为另一个 binomal queue,和原 binonal queue 删除 后的结果合并,应用上面的 Merge 算法即可。
3.2. Implementation
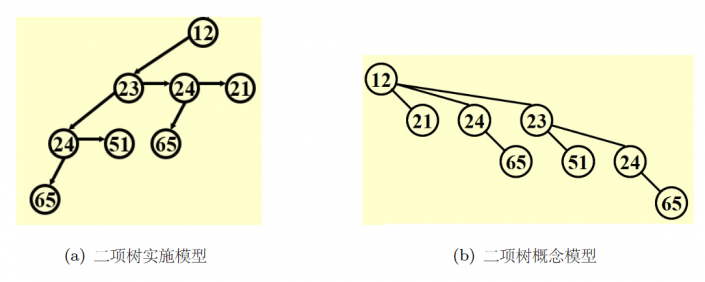
实现时为了方便快速实现孩子的顺序遍历,在存储孩子时可以考虑使用链表的方式,或者说,使用左儿子右兄弟(left-child , right-sibling) 的连接方式。
另一方面,我们的链表最好按照 的方法存储这些数,这样在合并的时候不用遍历孩子链表也能维持左儿子有兄弟的结构,具体自己画个图就知道了。
3.3. Complexity Analysis
A binomial queue of can be built by successive(连续) insertions in time. Claim
可以用均摊分析证明,具体证明过程略。