本篇笔记概述了二叉搜索树的基本概念及其变种，包括 AVL 树、Splay 树、红黑树和 B+ 树。首先介绍了 AVL 树的定义、插入和删除操作，以及如何维护树的平衡。接着讨论了 Splay 树的旋转操作和均摊分析，随后介绍了红黑树的插入和删除策略，最后讲解了 B+ 树的结构特性及其分裂和插入过程。整体上，笔记提供了对这些数据结构的深入理解和操作方法。（由 gpt-4o-mini 生成摘要）

1. AVL Tree

1. 空二叉树是一个 AVL 树(AVL tree)。
2. 如果 T 是一棵 AVL 树，那么其左右子树也是 AVL 树，并且 $|h(ls) - h(rs)| \le 1$，其中 $h(x)$ 是子树 $x$ 的高度。
3. 树高为 $O(\log n)$。

平衡因子(balance factor)：右子树高度 $-$ 左子树高度。（按照定义，对于任意节点都有 $BF(\text{node})=-1,0\text{ or } 1$）

1.1. Insertion

先与一般的二叉平衡树类似，先进行一次失败的查找，可以定位要插入的位置。插入的位置一定是一个叶子节点。之后自底向上检查有没有节点的平衡被破坏，如果有，其 $BF$ 值要么为 $-2$ 要么为 $2$。我们分类讨论进行调整。

称平衡被破坏的节点为失衡节点(trouble finder)，导致平衡被破坏的节点（即刚插入的节点）为肇事者(trouble maker)，只需要对于 trouble finder & maker 之间的子树进行调整。

在调整平衡时，我们只需要关注 trouble finder：

• 是左子树偏重（$BF = -2$）还是右子树偏重（$BF = 2$）？
• 是偏重的子树的左子树偏重还是偏重的子树的右子树偏重？

这里以左子树偏重（$BF = -2$）为例，右子树偏重的情况是对称的。当左子树的左子树偏重（$\text{height}[A]\ge \text{height}[C]$）时，需要执行单旋(single rotation)：

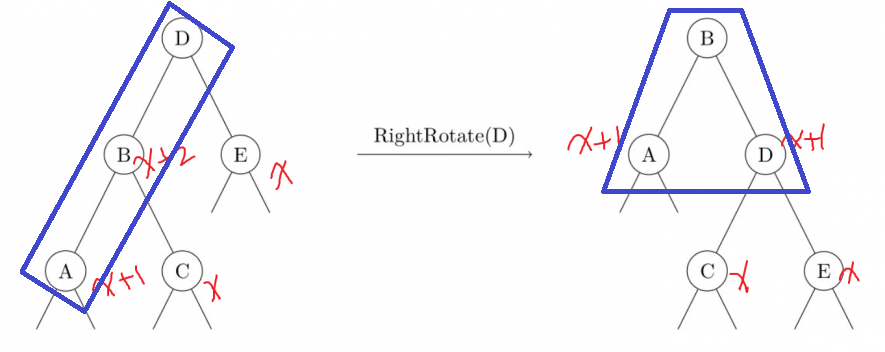单旋（红色标注的是树高）

当左子树的右子树偏重时（$\text{height}[A]< \text{height}[C]$），需要执行双旋(double rotation)：

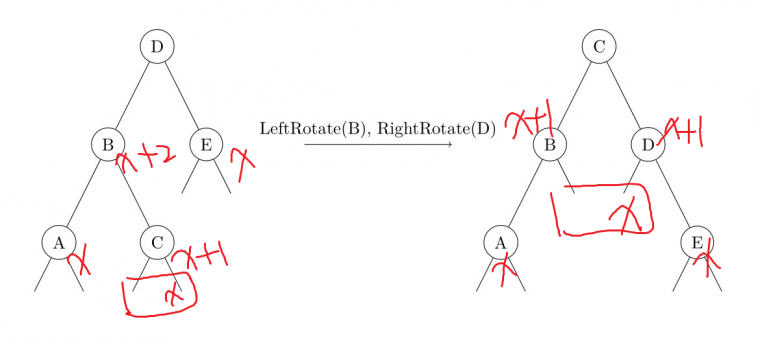双旋

容易发现，只需要在离 trouble maker 最近的 trouble finder 处进行一次单旋或双旋即可，因为旋转后 trouble finder 处的树高与插入节点前相同，在它上面的节点的 BF 值应与插入节点前相同。

维护平衡操作的伪代码如下：

Maintain-Balanced(p)
    if h[ls[p]] - h[rs[p]] == 2
        if h[ls[ls[p]]] >= h[rs[ls[p]]]
            Right-Rotate(p)
        else
            Left-Rotate(ls[p])
            Right-Rotate(p)
    else if h[ls[p]] - h[rs[p]] == -2
        if h[ls[rs[p]]] <= h[rs[rs[p]]]
            Left-Rotate(p)
        else
            Right-Rotate(rs[p])
            Left-Rotate(p)

1.2. Deletion

先定位要删除的节点，如果是叶子则直接删除，否则找到其前驱（左子树中最右的节点）或后继（右子树中最左的节点）将其替换。这样可以保证每次删除操作实际删掉的点一定是叶子。

删除节点后也要应用调整操作，维护平衡的方法类似插入操作。

2. Splay Tree

生长树(Splay Tree) 单次操作的均摊成本(averaged cost) 为 $O(\log n)$，但最坏情况下单次是 $O(n)$ 的。

2.1. Rotate

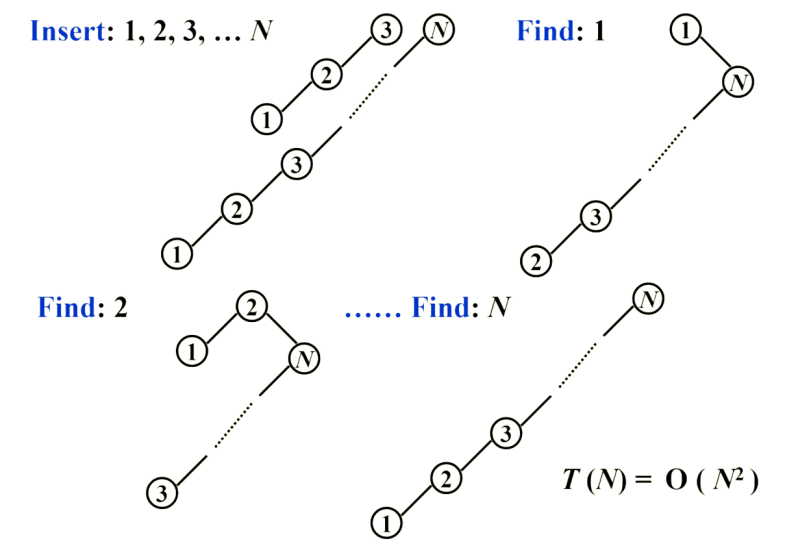
Splay 树的核心思想是每次将被访问的节点旋转到根，称为 Splay 操作。如果还是用前面的旋转方式，复杂度是可能被卡到 $O(n^2)$ 的：

这里需要引入 Splay 的旋转方式：设当前节点 $X$ 的父节点为 $P$，父节点的父节点为 $G$ 都存在。定义对 $X$ 的旋转操作 $Rotate(X)$ 为将 $X$ 旋转到 $P$ 的位置，即 $X$ 的父亲将变为 $G$，且维持平衡树的中序遍历不变。当 $X$ 是 $P$ 的左孩子时定义这样的旋转为右旋，当 $X$ 是 $P$ 的右孩子时定义这样的旋转为左旋。

（注意这里的 $Rotate$ 函数的参数和上文 AVL 树中的说法并不一样，即 $Rotate(X)$ 对应着 $LeftRotate(P)$ 或 $RightRotate(P)$，至于到底是哪个取决于 $X$ 和 $P$ 的位置关系。相当于一个说的时转上来，另一个说的是转下去，所以还需要讨论是从左边还是右边下去）

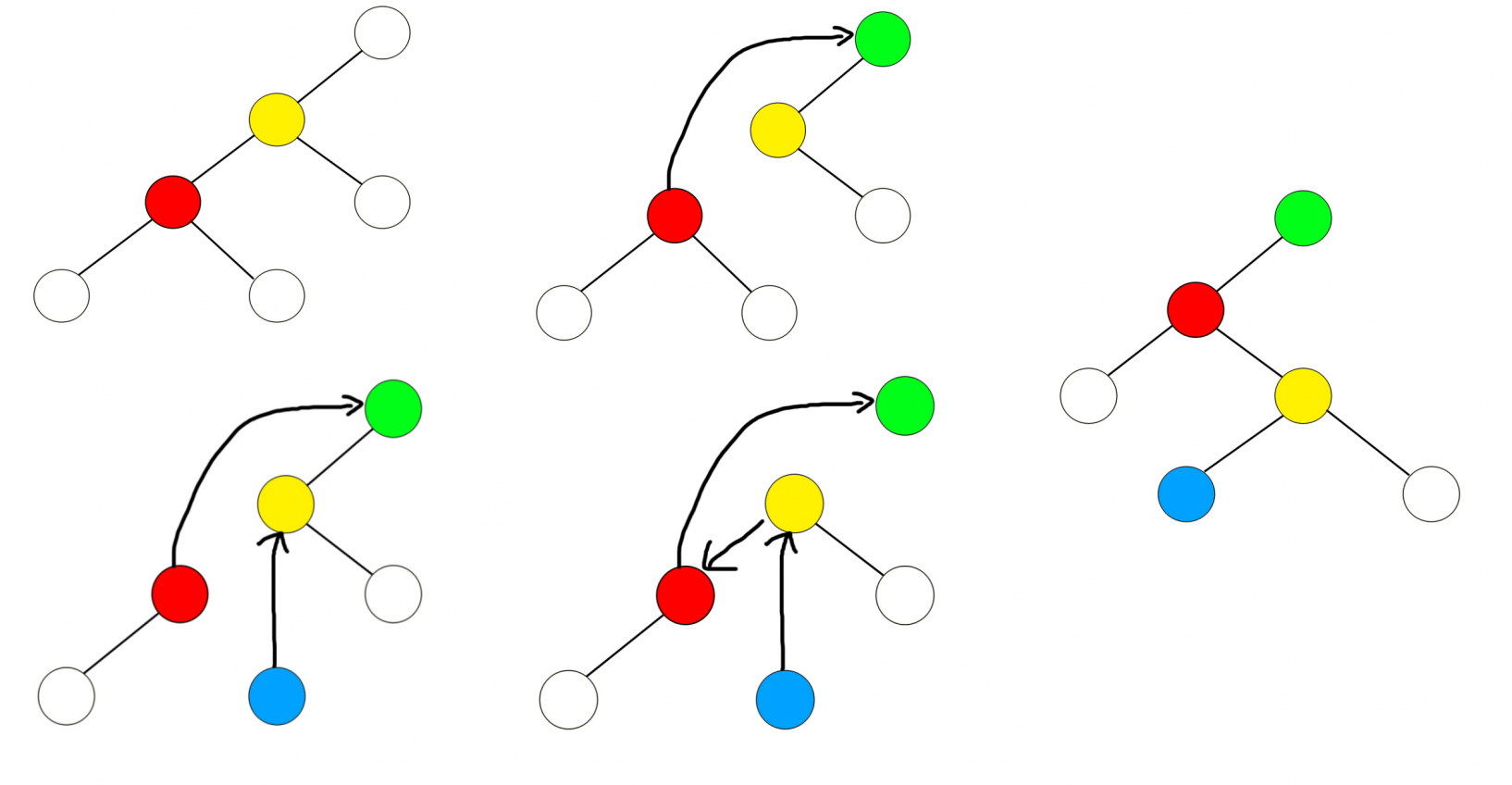（这里红色节点代表 X，黄色节点代表 P）

可以通过精巧的实现让代码自行决定左旋还是右旋，下文我们也直接用 $Rotate$ 操作来表示（自动决定的）左旋或右旋。

接下来：讨论 $X,P,G$ 是否在同一直线上。若在，则应用 Zig-Zig 操作，旋转 $Rotate(P),\,Rotate(X)$（虽然旋转的不是同一个点，但是两次旋转的方向相同）：

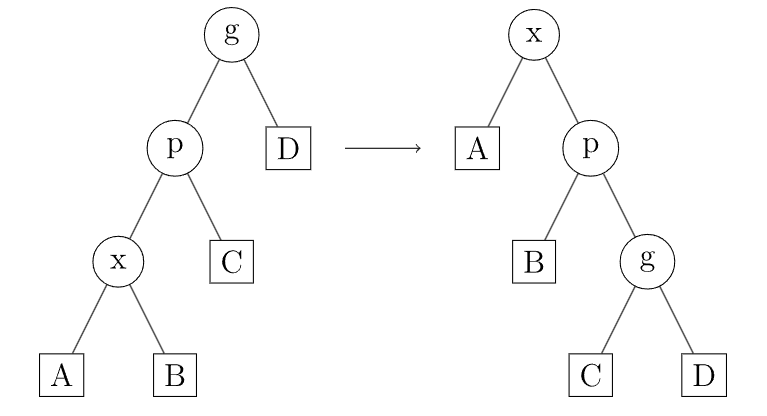Zig-Zig

若不在，则应用 Zig-Zag 操作，旋转 $Rotate(X),\,Rotate(X)$（虽然都是旋转同一个点，但是两次旋转的方向不同）：

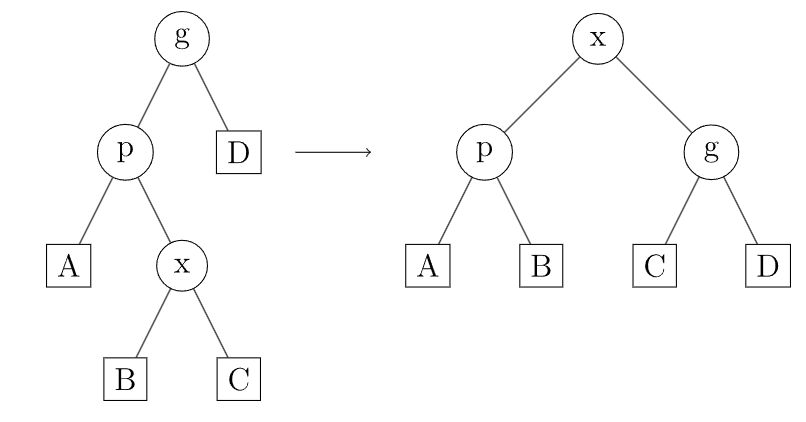Zig-Zag

这样子 Splay 树的复杂度将会得到保证，具体证明参见下面的均摊分析(amortized analysis) 环节。

2.2. Amortized Analysis

均摊分析(amortized analysis) 分为三种：

• 聚合分析(aggregate analysis)：总时间复杂度为 $T(n)$，则单次操作的均摊复杂度为 $T(n)/n$。
• 核算法(accounting method)：每消耗 $1$ 的时间进行操作，就为之后的操作累计 $1$ 的信用。操作要么消耗时间要么消耗信用。
• 势能法(potential method)：利用势能函数进行分析。

现在问题的关键在于确定势能函数。如果简单的将节点高度和定义为势能函数，虽然量级正确了，但是在 Splay 的过程中有许多节点的高度会发生变化，且数量不确定，这样定义的势能函数很难分析。

一个可用的势能函数是树中所有节点的 $\text{rank}$ 之和，我们用 $R(i)$ 表示节点 $i$ 的 $\text{rank}$，有

TBD

3. Red Black Tree

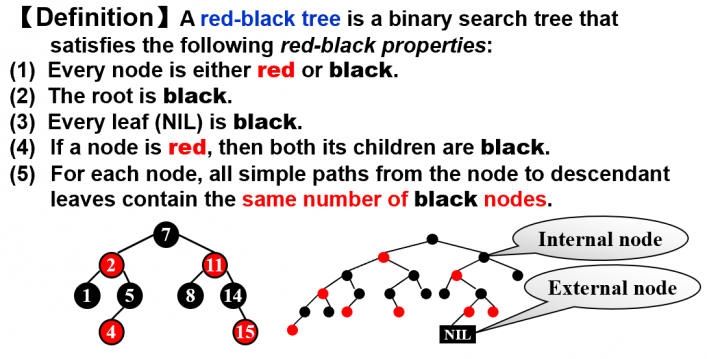
• 每条从叶子到根的路径中黑节点数 $\geq$ 红节点数。
• 每个叶子结点的左右指针都指向 NIL，定义 NIL 都是黑节点。——补上 NIL 后，整棵树中的黑节点数 $\geq$ 红节点数。

作出以下定义：

• The black-height of any node $x$, denoted by $bh(x)$：从节点 $x$ 到任意叶子的最短路径上的黑点数量。

3.1. Insertion

这里介绍 bottom-up 的插入方法。红黑树是存在 top-down 的插入方式的，但这里不展开。

• Step 1：先通过一次失败的查找确定要插入的位置（NIL 节点），将其替换为新节点并染成红色。由于新节点自带两个黑色的 NIL 结点，所以树的 black-height 不变，但可能出现连续的红节点。

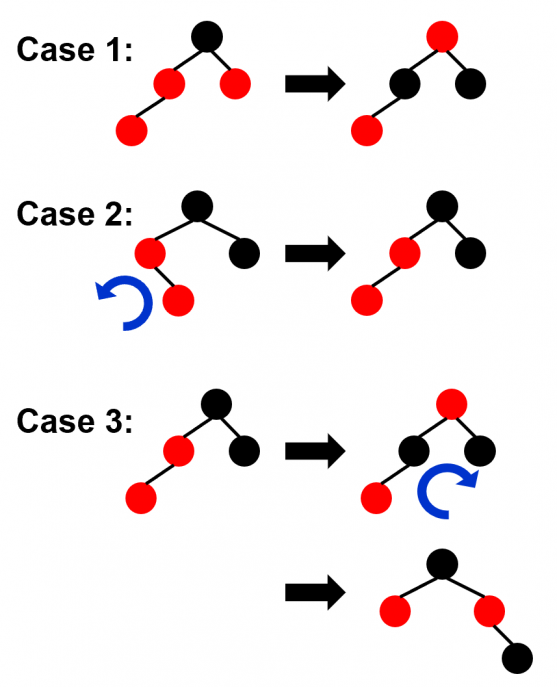
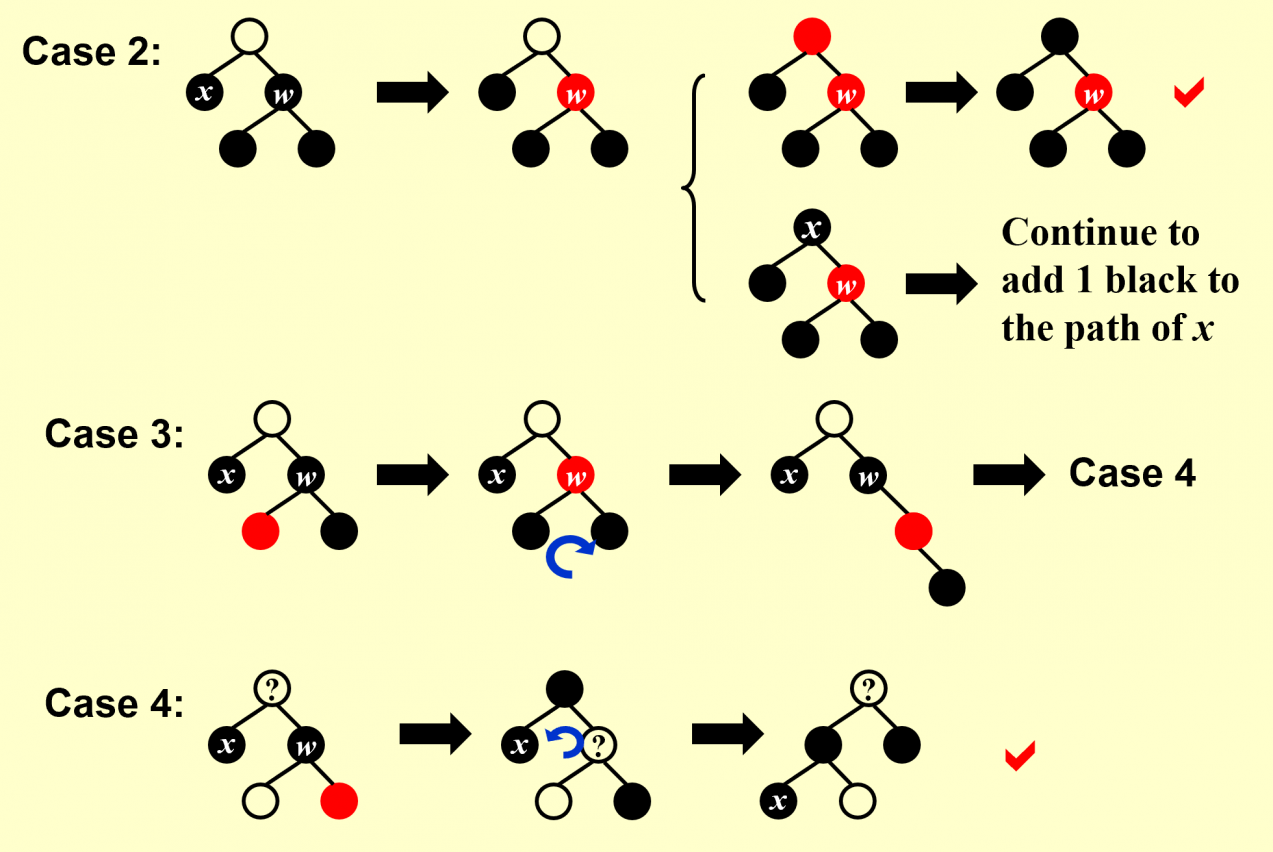
• Step 2：自底向上处理连续的红节点的问题，分以下三种情况讨论：

3.2. Deletion

• 兄红转兄黑。父兄换色兄旋升。（case 1）
• 兄黑远黑近侄红，侄兄换色侄旋升。（case 3）
• 兄黑远红化其黑，父兄换色兄旋升。（case 4）
• 兄侄全黑则兄红，黑父不当则上传。（case 2）

4. B+ Tree

定义：A B+ tree of order $M$ is a tree with the following structural properties:

• (1) The root is either a leaf or has between $2$ and $M$ children.
• (2) All non-leaf nodes (except the root) have between $\lceil M/2 \rceil$ and $M$ children.
• (3) All leaves are at the same depth.

可以注意到：

1. B+ 树的所有数据都存储在叶子节点，非叶节点只存储索引信息。
2. 每一个非叶节点上最多存储 $M-1$ 个索引，每一个叶子节点上最多存储 $M$ 个数据。
3. 对于非叶节点的第 $i$ 个索引，其值等于其第 $i+1$ 个子树的叶子节点最小值。（根据这一性质可以进行查找）

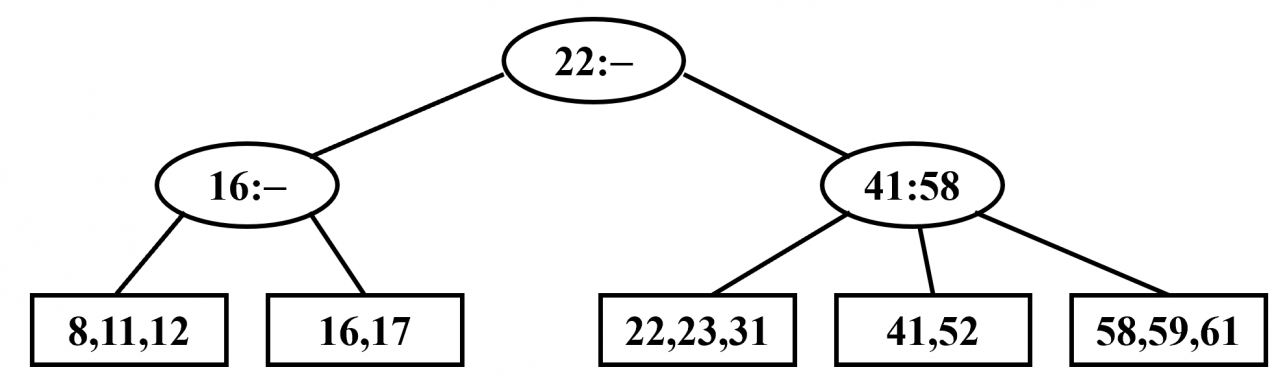B+ 树示意图

4.1. Split

B+ 树的核心在于其分裂操作。可以把 $M$ 的限制看做对连出去的边数的限制，叶子节点相当于是连出去至多 $M$ 条节点—数据的边，这样可以把非叶节点和叶子节点的情况统一看待。

当某个节点已经连出去 $M$ 条边，需要塞第 $M+1$ 条边的时候，需要分裂。分裂会产生一个和原节点同级的节点，就在原节点的右侧。原节点的前 $\lceil(M+1)/2\rceil$ 个孩子还属于自己，剩下的 $\lfloor(M+1)/2\rfloor$ 个孩子需要交给新创建的节点。

如果分裂的过程中，导致父节点也超出了 $M$ 的限制，就需要对父节点也进行分裂，以此类推。如果父节点已经是根节点，就创建一个新根再进行分裂，此时树高会增加 $1$，其他情况下树高不会改变。

4.2. Insertion

先进行一次查找确定需要插入的节点并执行挂在那个叶子节点上，接下来进行 bottom-up 的维护即可。

课件中给出的伪代码

4.3. Complexity Analysis

一般来说我们取 $M=3$（2-3 树）或 $M=4$（2-3-4 树）。当 $M$ 不是常数级别时，需要用二分查找对插入过程进行优化。

TBD：复杂度分析